ayuda por favor, es una operación con Fracción:")​

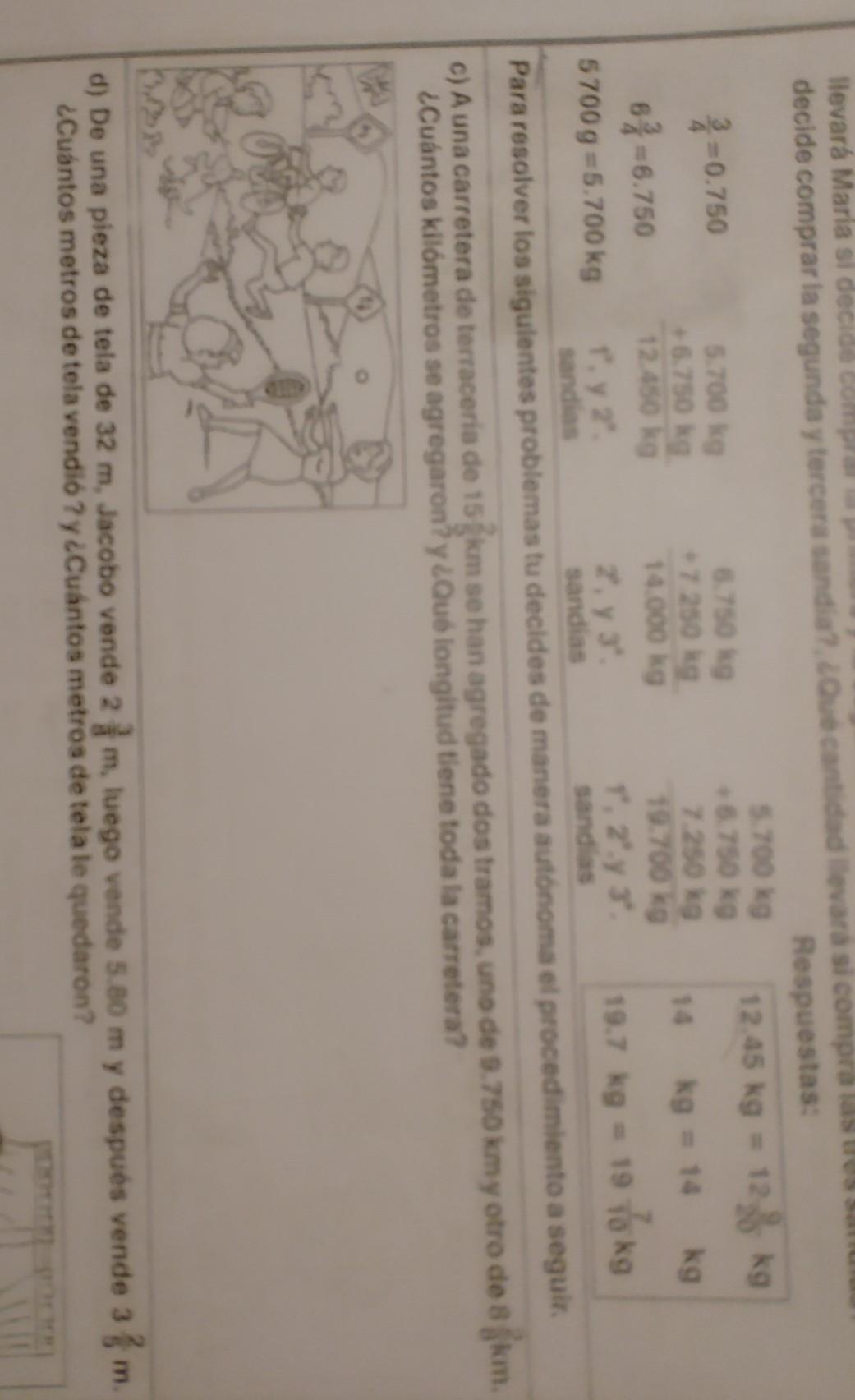
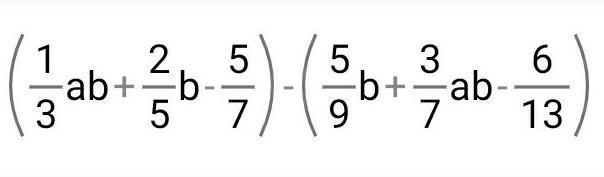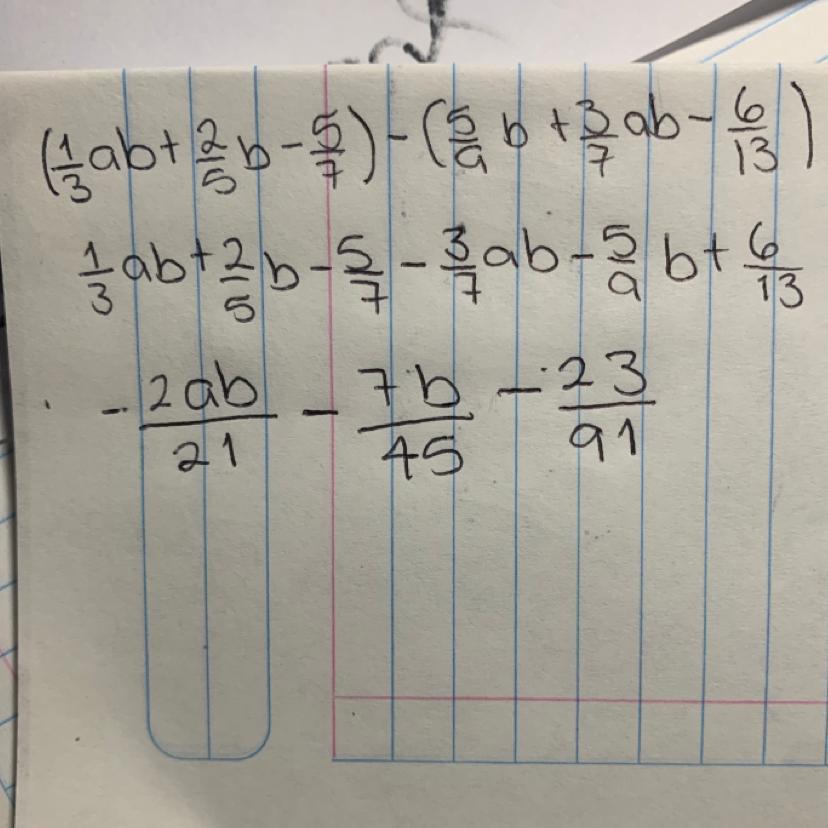Para encontrar la ecuación de la parábola con directriz horizontal, necesitamos utilizar la definición de la parábola en términos de la distancia desde el foco y la directriz:

La parábola es el lugar geométrico de todos los puntos que equidistan de una recta fija llamada directriz y un punto fijo llamado foco.

En este caso, la directriz es la recta L1: x - y + 1 = 0, que tiene pendiente 1, y el foco es la recta L2: x + y + 3 = 0, que tiene pendiente -1.

El vértice de la parábola está sobre la recta L1, que tiene pendiente 1. Si trazamos una línea perpendicular a L1 desde el punto medio entre L1 y L2, obtendremos la recta que contiene al eje de simetría de la parábola y que también pasa por el vértice. La pendiente de esta recta será la negativa del recíproco de la pendiente de L1.

El punto medio entre L1 y L2 se encuentra resolviendo el sistema de ecuaciones:

x - y + 1 = 0

x + y + 3 = 0

Restando estas dos ecuaciones, obtenemos:

-2y - 2 = 0

De donde se deduce que y = -1. Sustituyendo este valor en cualquiera de las dos ecuaciones, obtenemos que x = -2.

Por lo tanto, el punto medio entre L1 y L2 es (-2, -1).

La pendiente de L1 es 1, por lo que la pendiente de la recta que contiene al eje de simetría es -1. Como esta recta pasa por el vértice (que está sobre L1 en algún punto desconocido), podemos utilizar la ecuación de la recta para encontrar su ecuación:

y + 1 = -1(x + 2)

y = -x - 3

Este es el eje de simetría de la parábola. Ahora necesitamos encontrar la distancia entre el foco y la directriz.

Podemos hacer esto notando que la distancia desde un punto (x, y) a una recta ax + by + c = 0 es:

d = |ax + by + c| / sqrt(a^2 + b^2)

Por lo tanto, la distancia desde un punto (x, y) a la directriz L1 es:

d1 = |x - y + 1| / sqrt(2)

Y la distancia desde un punto (x, y) al foco L2 es:

d2 = |x + y + 3| / sqrt(2)

Como la parábola es el lugar geométrico de los puntos que equidistan de la directriz y el foco, podemos igualar estas dos distancias:

| x - y + 1 | / sqrt(2) = | x + y + 3 | / sqrt(2)

Despejando |x - y + 1| y elevando al cuadrado ambos lados de la ecuación, obtenemos:

(x - y + 1)^2 = (x + y + 3)^2

Expandiendo y simplificando esta ecuación, obtenemos:

4x = 6y + 16

O, equivalentemente:

y = (2/3)x - 8/3

Respuesta:

We can start by simplifying the left side of the equation using the identity: (a - b)^2 = a^2 - 2ab + b^2.

√(5 - x)^2 + 64 = 10 => (5 - x)^2 + 64 = 100 (squaring both sides to eliminate the square root) => (5 - x)^2 = 36 => 5 - x = ±6 (taking the square root of both sides and solving for x) => x = 5 - 6 or x = 5 + 6

Therefore, the solutions are x = -1 and x = 11.

Respuesta:

La creación del Virreinato de Nueva Granada en 1717 tuvo dos consecuencias inmediatas para el espacio quiteño: la incorporación de su distrito a la nueva jurisdicción y la supresión de su Audiencia. Estas dos medidas afectaron, además de a otras instancias, a la Real Hacienda de Quito.

Explicación:

Respuesta:

te puedo ayudar pero no con todas te sirve