me lo pueden resolver doy coronita ​

Respuesta:204

Explicación paso a paso:

se multiplica 391 por 12 entre 23 y da el resultedo

Respuesta:

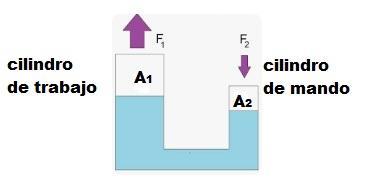
De acuerdo al principio de Pascal, en una prensa hidráulica la presión aplicada en un punto se transmite de manera uniforme en todas las direcciones y en todas las partes del fluido, lo que permite amplificar la fuerza aplicada.

Si la prensa está diseñada para amplificar 100 veces la fuerza F1, entonces la relación entre la fuerza en el cilindro de mando y la fuerza en el cilindro del trabajo es:

F2 = 100 x F1

Además, la presión en el fluido es la misma en ambos cilindros, por lo que podemos utilizar la fórmula de la presión en un fluido:

P = F / A

donde P es la presión, F es la fuerza y A es el área en la que se aplica la fuerza.

Si consideramos los dos cilindros como si fueran un solo fluido, podemos igualar las presiones en ambos cilindros:

P1 = P2

Reemplazando las fórmulas de presión en términos de fuerza y área, tenemos:

F1 / (π x R1^2) = F2 / (π x R2^2)

Reemplazando F2 por su valor en términos de F1, tenemos:

F1 / (π x R1^2) = (100 x F1) / (π x R2^2)

Simplificando, tenemos:

R2^2 = 100 x R1^2

Tomando la raíz cuadrada de ambos lados, obtenemos:

R2 = 10 x R1

Por lo tanto, el radio R2 del cilindro del trabajo debe ser 10 veces mayor que el radio R1 del cilindro de mando para que la prensa hidráulica amplifique 100 veces la fuerza aplicada.

Explicación:

La premilitar es un programa educativo que se enfoca en la preparación física, moral y cívica de los jóvenes antes de su incorporación al servicio militar. Las posiciones fundamentales en premilitar son las posiciones básicas que se enseñan en la formación militar. A continuación se presentan seis características de las posiciones fundamentales en premilitar:

Son universales: las posiciones fundamentales en premilitar son las mismas en todas las fuerzas armadas y son utilizadas en todo el mundo.

Son simples: las posiciones fundamentales en premilitar son muy sencillas y fáciles de aprender. Estas posiciones no requieren una habilidad especial y cualquier persona puede aprenderlas.

Son importantes: las posiciones fundamentales en premilitar son muy importantes para la formación militar. Son la base de la disciplina, el orden y la organización.

Son precisas: las posiciones fundamentales en premilitar requieren precisión y exactitud en su ejecución. Es importante que se hagan correctamente para que se logre una buena formación.

Son útiles: las posiciones fundamentales en premilitar son muy útiles en situaciones de emergencia y en operaciones militares. Estas posiciones permiten una organización rápida y eficiente de los soldados en el campo de batalla.

Son requeridas: las posiciones fundamentales en premilitar son requeridas en todos los entrenamientos y prácticas militares. Los soldados deben conocer y dominar estas posiciones para poder desempeñarse de manera efectiva en situaciones de emergencia o en operaciones militares