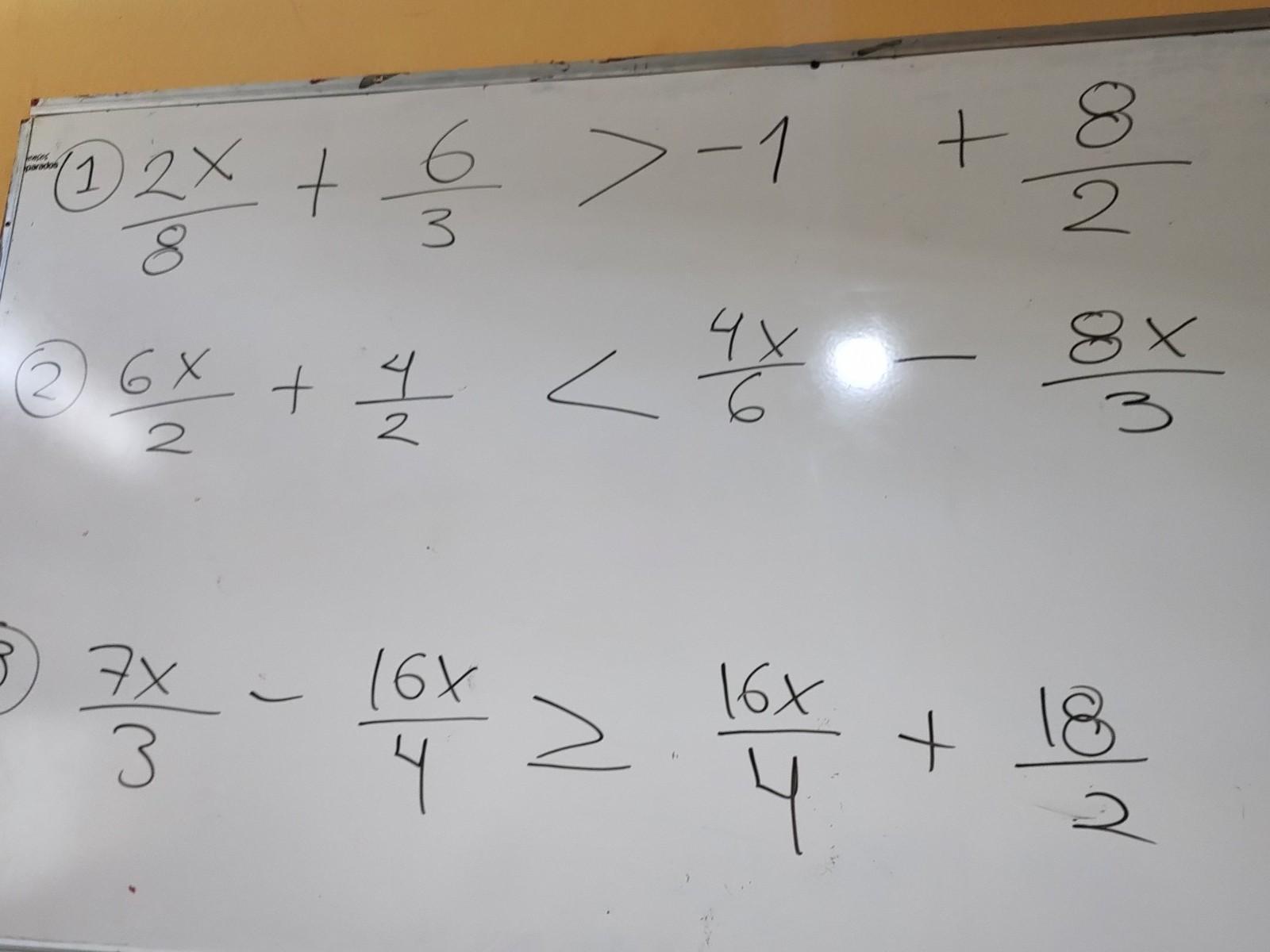Es sencillo resolver inecuaciones, solo basta con operar como si fueran ecuaciones comunes, el signo "<" o ">" solo nos sirve cuando vallamos a graficar o determinar el valor de "x" fuera de eso, no tiene otro valor en la ecuación como tal, más que confundir al alumno.
Nota antes de empezar:
Fracción Homogénea : Cuando el determinador de una o varias fracciones son iguales.
5/3 ; 17/3 ; 151/3 ; etc.
Problema 1:
\frac{2X}{8} + \frac{6}{2} > -1 +\frac{8}{2}
Ahora vemos si podemos simplificar cada fracción para poder operar más cómodamente:
\frac{2X}{8} + \frac{6}{2} > -1 +\frac{8}{2} (Notamos que tanto en el primer miembro (izquierda del ">") , como en el segundo miembro (derecha del ">") hay cosas que podemos simplificar, así que lo hacemos)
Este sería la nueva apariencia del problema:
\frac{X}{4} + 3 > -1 + 4
Ahora es más sencillo de operar.
\frac{X}{4} + 3 > -1 + 4
\frac{X}{4} + 3 > 3
Procedemos a sumar a ambos lados "-3" para eliminar el "+3" del lado izquierdo y dejar a la variable sola.
\frac{X}{4} + 3 > 3
\frac{X}{4} + 3 -3 > 3 - 3
\frac{X}{4} > 0
Ahora multiplicamos a ambos lados por el numero 4, para eliminar la división entre 4 que esta afectando a la variable.
\frac{X}{4} > 0
\frac{X}{4} . 4 > 0 .4
X > 0
Problema 2 :
\frac{6X}{2}+\frac{4}{2} < \frac{4X}{6}-\frac{8X}{3}
Aquí como primer paso vemos si hay algo que podamos "simplificar" , en caso no hubiera se procede a operar.
\frac{6X}{2}+\frac{4}{2} < \frac{4X}{6}-\frac{8X}{3}
Simplificando:
\frac{6X}{2}+\frac{4}{2} < \frac{4X}{6}-\frac{8X}{3}
3X+2 < \frac{2X}{3}-\frac{8X}{3}
Ahora , ya podemos operar, pero vemos algo curioso en el segundo miembro (lado derecho) ,que hay 2 fracciones homogéneas, lo cual nos facilita todo, ya que podemos sumar (o restar) los numeradores directamente.
3X+2 < \frac{2X}{3}-\frac{8X}{3} = 3X+2 < \frac{2X-8X}{3} = 3X+2 < \frac{-6X}{3}= 3X+2 < -2X
Nos quedaría así :
3X+2 < -2X
Ahora procedemos a operar:
3X+2 < -2X
Sumamos a ambos lados "2x" para eliminar el "-2x" del lado derecho.
3x+2 + 2x < -2x + 2x
5x+2 < 0
ahora sumamos "-2" a ambos lados para eliminar el "+2" que esta del lado izquierdo.
5x+2-2 < 0 - 2
5x < -2
Ahora dividimos ambos lados por el numero 5, para eliminar el 5 que esta multiplicando a la variable.
\frac{5X}{5} < \frac{-2}{5}
X < -\frac{2}{5}
X < - 0,4
Problema 3:
\frac{7X}{3} - \frac{16}{4} ≥ \frac{16X}{4} + \frac{18}{2}
Primero procedemos a simplificar.
\frac{7X}{3} - \frac{16}{4} ≥ \frac{16X}{4} + \frac{18}{2}
Simplificado :
\frac{7X}{3} - 4 ≥ 4X + 9
Ahora procedemos a operar.
\frac{7X}{3} - 4 ≥ 4X + 9
Sumamos a ambos lados un "+4" para liminar el "-4" que esta del lado izquierdo.
\frac{7X}{3} - 4+4 ≥ 4X + 9+4
\frac{7X}{3} ≥ 4X + 13
Ahora multiplicamos a ambos lados por el numero 3 para eliminar del lado izquierdo la división que esta afectando a la variable.
\frac{7X}{3} ≥ 4X + 13
\frac{7X}{3}.3 ≥ (4X + 13).3
7x ≥ 12X + 39
Ahora sumamos un "-7X" a ambos lados para liminar el "7x" que esta del lado izquierdo.
7X -7X ≥ 12X+39-7X
0 ≥ 5X + 39
Ahora sumamos a ambos lados un "-39 para poder eliminar el "+39" del lado derecho y dejar solo a la variable.
0 - 39 ≥ 5X +39 - 39
-39 ≥ 5X
Ahora dividimos ambos lados por el numero 5.
-\frac{39}{5} ≥ \frac{5X}{5}
-\frac{39}{5} ≥ X
-7,8 ≥ X
Espero haber ayudado, si crees que mi respuesta te ayudo no dudes en darme una corona.