escribe los principales hechos que ocurrieron en cada uno de los viajes de pizarro

Respuesta:

Daniel gratefully accepted his prestigious award

Tina declined the surprising job offer politely

The next day was surprisingly hot

That was an incredibly stupid thing to do

Paragliding was an absolutely unforgettable experience

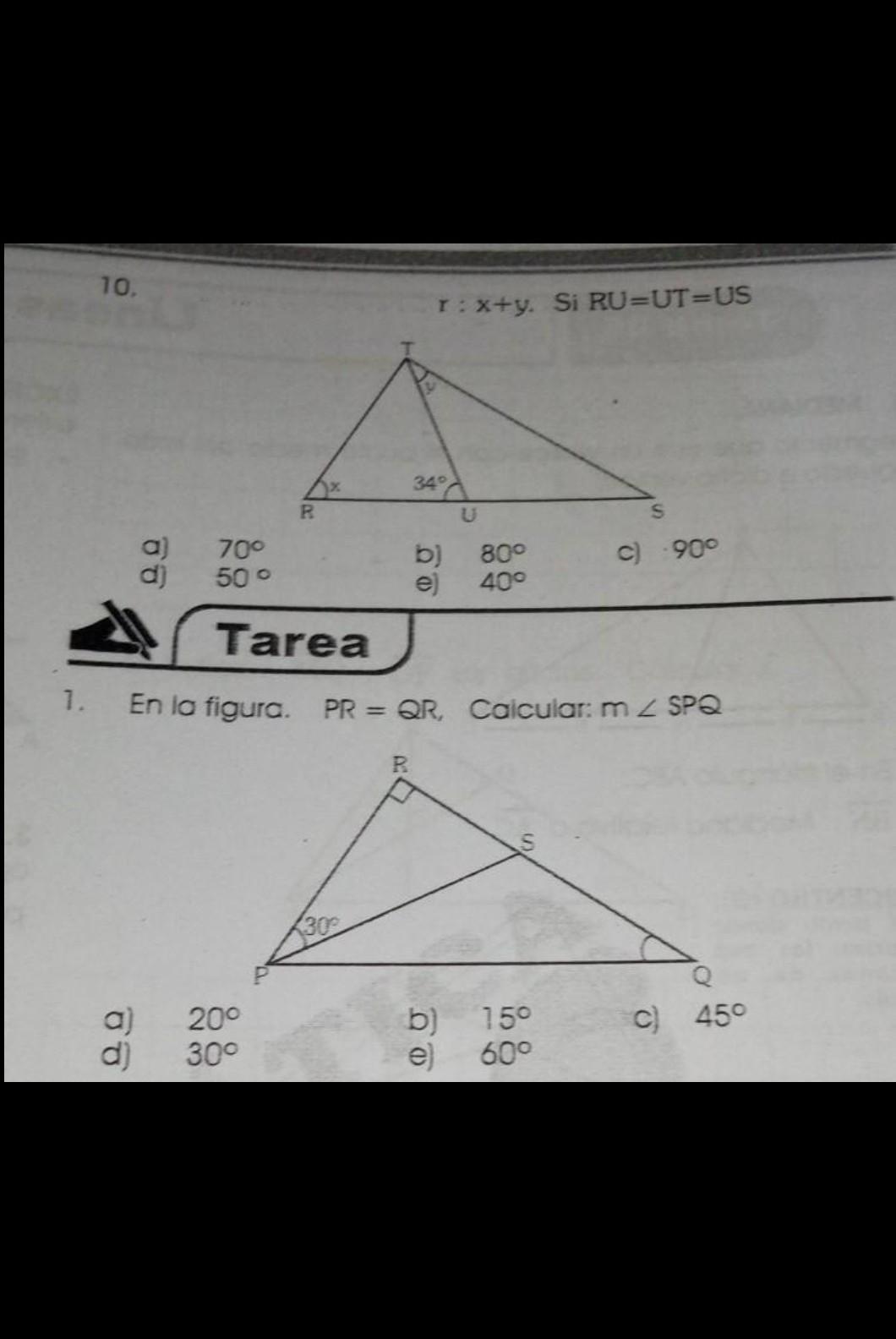
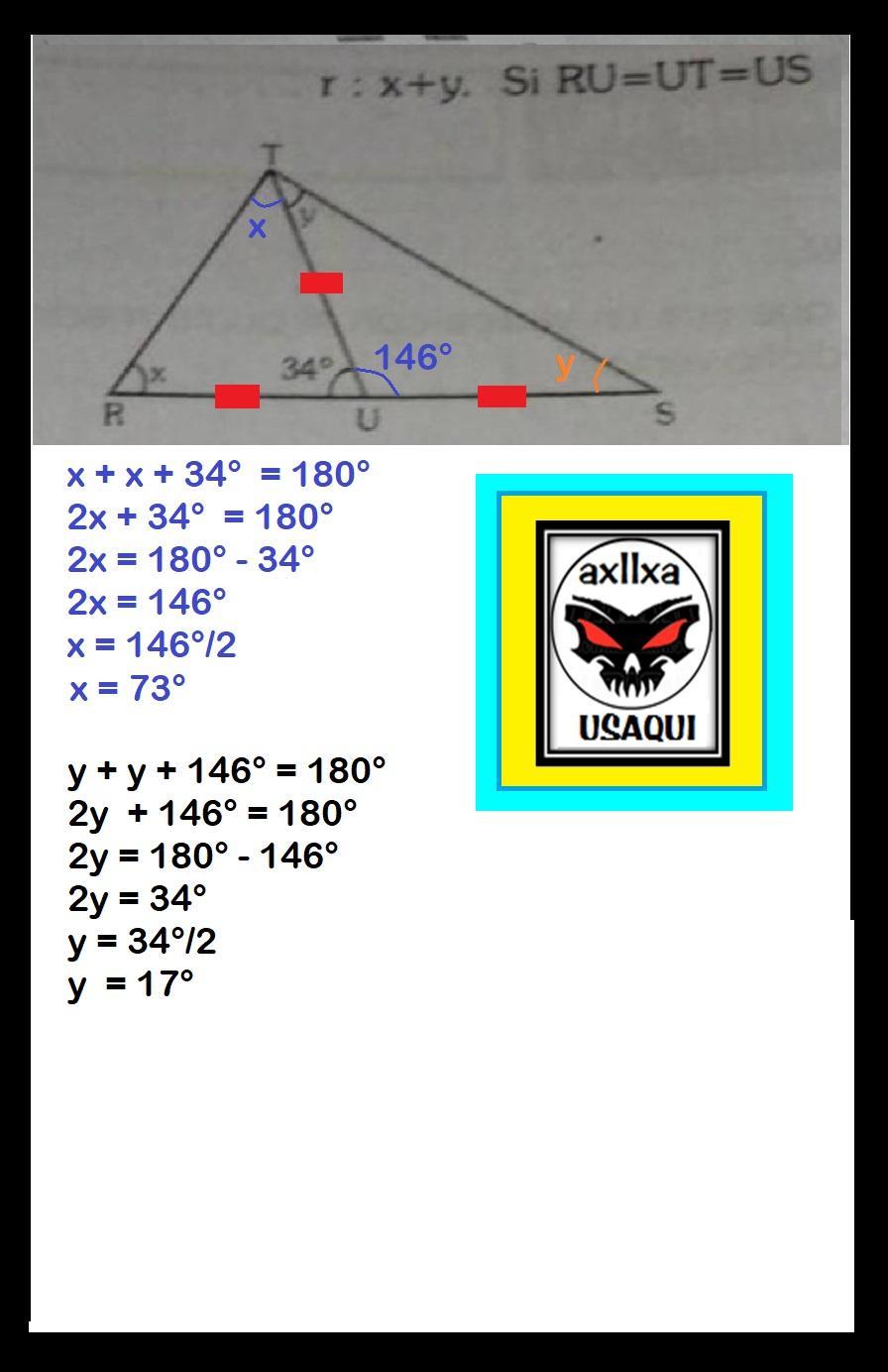
Respuesta:

Explicación paso a paso:

Para resolver el problema, utilizaremos las fórmulas siguientes:

a) La suma de los ángulos externos de cualquier polígono siempre es 360°. Como un polígono regular tiene todos sus ángulos y lados iguales, podemos encontrar la medida del ángulo externo dividiendo 360° entre el número de lados del polígono:

ángulo externo = 360° / número de lados

b) La suma de los ángulos centrales de cualquier polígono siempre es 360°. Como un polígono regular tiene todos sus ángulos y lados iguales, podemos encontrar la medida del ángulo central dividiendo 360° entre el número de lados del polígono:

ángulo central = 360° / número de lados

c) La suma de los ángulos interiores de un polígono regular de n lados viene dada por la fórmula:

suma de los ángulos interiores = (n - 2) x 180°

Como todos los ángulos interiores de un polígono regular tienen la misma medida, podemos encontrar la medida de cada uno dividiendo la suma de los ángulos interiores entre el número de lados del polígono:

ángulo interior = suma de los ángulos interiores / número de lados

a) La medida del ángulo externo es:

ángulo externo = 360° / número de lados

Podemos obtener el número de lados dividiendo 360° entre la medida del ángulo interno:

número de lados = 360° / ángulo interno

número de lados = 360° / 168.75°

número de lados = 2.133

Como el número de lados debe ser un número entero, podemos concluir que no existe un polígono regular con un ángulo interno de 168.75°.

b) Si existiera un polígono regular con un ángulo interno de 168.75°, la medida del ángulo central sería:

ángulo central = 360° / número de lados

ángulo central = 360° / 2.133

ángulo central = 168.75°

c) Como se ha demostrado que no existe un polígono regular con un ángulo interno de 168.75°, no podemos determinar el número de lados.

Nota: Si crees que mi respuesta es merecedora de 5 estrellas me las puedes dar.

a.3/50

b.6/50

c.14/50

d.38/50

e.3/50

☆༒ Eternamente axllxa ༒☆