La altura de la torre es de 28 metros
Se trata de un problema de razones trigonométricas en triángulos rectángulos.
Las razones trigonométricas de un ángulo α son las razones obtenidas entre los tres lados de un triángulo rectángulo.
Donde el triángulo de 30-60 es un triángulo notable
Dado que desde lo alto de un edificio se observa la parte inferior de una torre con un ángulo de depresión de 60° y la parte superior de la misma con un ángulo de elevación de 30°:
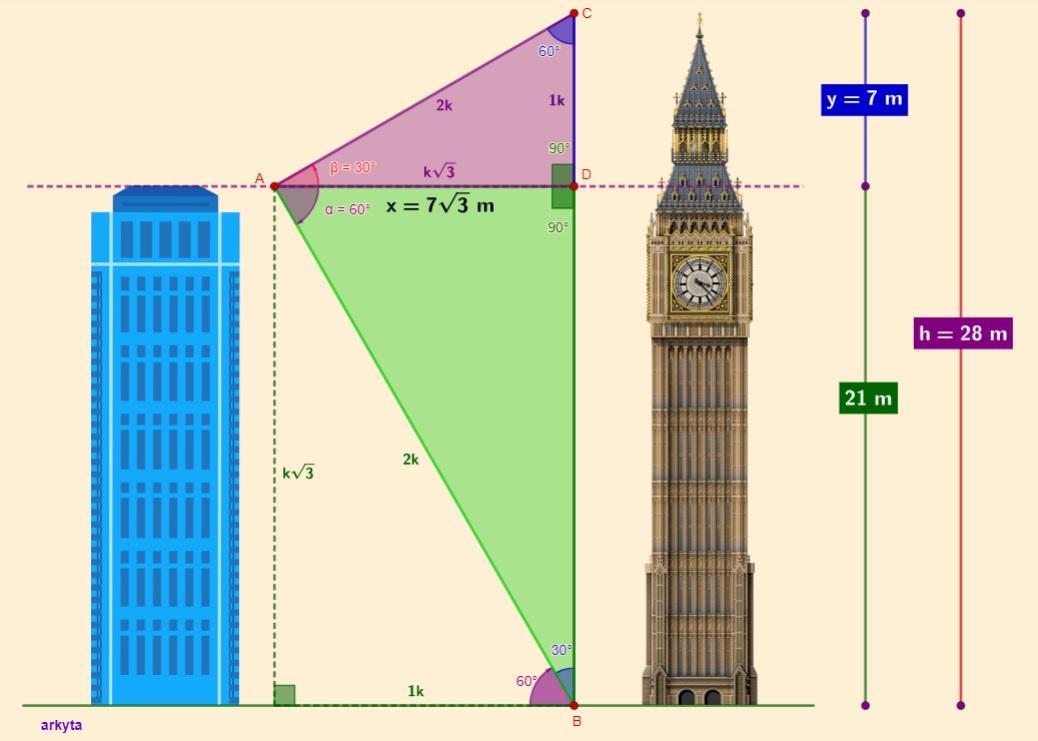
Representamos la situación en dos triángulos rectángulos:
El ABD: en donde el lado AB representa la línea visual -que está por debajo de los ojos del observador- a la parte inferior de la torre-, vista con un ángulo de depresión de 60°, el lado DB que es una porción de la altura de la torre y a la vez coincide con la altura de la azotea del edificio en donde se encuentra el observador, siendo el cateto opuesto al ángulo dado de este triángulo, y por último el lado AD que es la línea horizontal de visión a la torre y también la distancia horizontal hasta esta, en donde este otro cateto -es en este caso el adyacente-, -de la cual no conocemos su magnitud a la que llamamos distancia "x"- , la cual es una preincógnita
El ACD: en donde el lado AC representa la línea visual -que está por encima de los ojos del observador- a la parte superior de la torre-, vista con un ángulo de elevación de 30°; el lado CD que es el cateto opuesto al ángulo dado en este triángulo y que equivale a la otra porción de la altura de la torre, -de la cual no conocemos su dimensión y la llamamos distancia "y"- ; teniendo finalmente el lado AD el cual es el cateto adyacente al ángulo, y coincide con el cateto adyacente del primer triángulo, siendo la distancia "x" desde el edificio hasta la torre
Donde se pide hallar la altura "h" de la torre observadaPor tanto se determinará primero la distancia "x" -desde el edificio hasta la torre-, y una vez conocida esa distancia calcularemos la distancia "y"
Donde hallada la distancia "y" en el segundo triángulo -siendo el cateto opuesto del mismo:
La sumatoria de los dos catetos opuestos a los ángulos dados de cada uno de los dos triángulos nos dará la altura "h" de la torreDado que la tangente de un ángulo se define como la razón entre el cateto opuesto y el cateto adyacente:
Se empleará la razón trigonométrica tangente en cada uno de los dos triángulos rectángulos para determinar las distancias "x" e "y"
Razones trigonométricas con ángulos notablesEn ABDHallamos x - distancia desde el edificio hasta la torre-Por ser ángulo alterno interno- que es homólogo- se traslada el ángulo de depresión de 60° al punto B para facilitar la situación
Por ello se han trazado dos proyecciones horizontales
Relacionamos los datos con la tangente del ángulo α \bold{\alpha = 60^o}
\boxed{\bold { tan(60^o) = \frac{ cateto\ opuesto }{ cateto\ adyacente } } }
\boxed{\bold { tan(60^o) = \frac{ altura\ edificio }{ distancia \ x } } }
\boxed{\bold { distancia \ x = \frac{ altura\ edificio }{ tan(60^o) } } }
\large \textsf{El valor exacto de tan de 60 grados es } \bold {\sqrt{3} }
\boxed{\bold { distancia \ x = \frac{21 \ m }{ \sqrt{3} } } }
\boxed{\bold { distancia \ x = \frac{21}{\sqrt{3} } \ m } }
\boxed{\bold { distancia\ x = \frac{21}{ \sqrt{3} } \ .\ \frac{ \sqrt{3} }{ \sqrt{3} } \ m } }
\boxed{\bold { distancia\ x = \frac{21 \sqrt{3} }{( \sqrt{3})^{2} } \ m } }
\boxed{\bold { distancia\ x = \frac{21 \sqrt{3} }{3 } \ m } }
\boxed{\bold { distancia\ x = \frac{7\ . \not3 \sqrt{3} }{\not3 } \ m } }
\large\boxed{\bold { distancia \ x = 7\sqrt{3} \ metros } }
La distancia desde el edificio hasta la torre es de 7√3 metrosConocido el valor de la preincógnita x
En ACDHallamos y - porción de la altura de la torre-Relacionamos los datos con la tangente del ángulo β \bold{\beta =30^o }
\boxed{\bold { tan(30^o) = \frac{ cateto\ opuesto }{ cateto\ adyacente } } }
\boxed{\bold { tan(30^o) = \frac{ distancia \ y }{ distancia \ x } } }
\boxed{\bold { distancia \ y = distancia \ x \ . \ tan(30^o ) } }
\large \textsf{El valor exacto de tan de 30 grados es } \bold {\frac{ \sqrt{3} } {3 } }
\boxed{\bold { distancia \ y = 7\sqrt{3} \ m \ . \ \frac{ \sqrt{3} }{ 3} } }
\boxed{\bold { distancia \ y = 7 \ . \ \frac{ (\sqrt{3})^{2} }{ 3} m } }
\boxed{\bold { distancia\ y = \ \frac{7 \ . \not3 }{\not3 } \ m } }
\large\boxed{\bold { distancia \ y = 7 \ metros } }
La distancia y es de 7 metros- siendo una parte de la altura de la torre-
Hallamos la altura h de la torre\boxed{\bold { Altura \ Torre\ (h) = altura\ edificio\ +\ distancia \ y } }
\boxed{\bold { Altura \ Torre\ (h) = 21 \ m +\ 7 \ m } }
\large\boxed{\bold {Altura \ Torre\ (h) = 28 \ metros } }
La altura de la torre es de 28 metros
Se agrega gráfico a escala para mejor comprensión del ejercicio propuesto