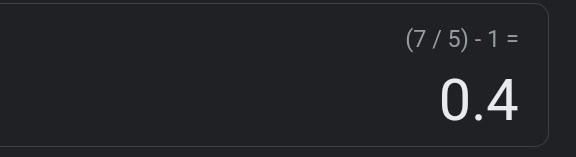
el resultado de 7/5-1 es igual a ?
-
Materia:
Estadística y Cálculo -
Autor/a:
mariacooper -
Creada:
hace 1 año
Respuestas 2
Respuesta:
2/5
Explicación:
7/5 - 5/5= 2/5
espero te sirva.
-
Autor/a:
fridacoffey
-
Califica una respuesta:
19
Respuesta:
no se si te ayudará pero
espero que te sirva :)
-
Autor/a:
americacnhu
-
Califica una respuesta:
4
¿Conoces la respuesta? Añádela aquí
Escoger idioma y región
How much to ban the user?
1 hour
1 day
100 years
