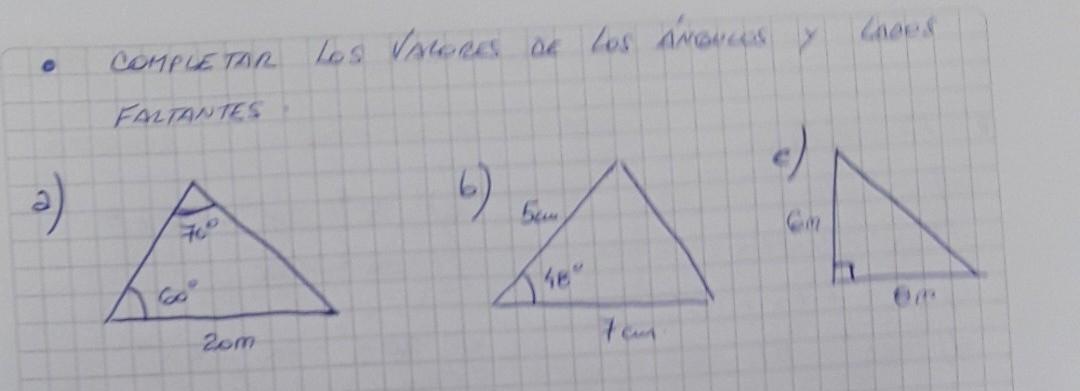
leo y escribo una explicación clara:"creer es un acto del entendimiento que asiente a la verdad divina por imperio de la voluntad movida por dios mediante la gracia" santo tomas de equino ​

Respuestas 1

Respuesta:

a qué necesitas ayuda ??

¿Conoces la respuesta? Añádela aquí

Can't find the answer?

Other related questions that may help you

¿Cuál es el mayor número que divide a 24 y 36 a la vez?​

Respuesta:

12

divide a 24 / 12 = 2

36 / 12 = 3

espero te sirva :)<3

formas de manifestar la motivacion

para manifestar motivación necesitamos tener alguna inspiración ya sea por alguna meta o propósito k tengamos

AYUDAAA DOY CORONA Y 5 ESTRELLAS ​
question img

Respuesta: con ayuda de teorema de Pitágoras, Ley de Senos y Cosenos, y suma de ángulos interiores.

Explicación paso a paso:

x1/sin(60) = 20/sin(70) -> x1=18,4 m (lado opuesto a 60°)x2/sin(180-130) = 20/sin(70) -> x2=16,3 m (lado opuesto a 50°)

angulo que falta= 180 - (70+60) = 50°b) x^2=25+49-2*5*7*cos(48)x=5,2 cm (lado faltante)

5/sin(angulo2)=5,2/sin(48) -> sin(angulo2)=5*sin(48)/5,2-> angulo2 = sin^(-1) ( 7*sin(48)/5,2)

-> angulo2= 45.48° (angulo opuesto  a 5 cm)-> angulo3= 180 - (48+ 45.48) = 86.52° (angulo opuesto a 7cm)

c) h^2 = 64+36 -> h=10 m (lado faltante)

6/sin(angulo2) = 10/sin(90) -> sin(angulo2) =6*1/10 = 3/5

-> angulo2 = sin^(-1)(3/5) -> angulo2=36.87° (angulo opuesto a 6m)

-> angulo3=180-(90+36.87) -> angulo3=53.13° (angulo opuesto a 8m)

las tortugas recientemente estan en peligro de extinción donde se encuentra el adverbio​

Respuesta:

El adverbio en esta oración es "recientemente". Modifica al verbo "están" y nos indica cuándo ocurrió la situación de las tortugas estar en peligro de extinción.

Explicación:

Respuesta:

el adverbio significa van lento

Other Filosofía Questions

Iniciar sesión con Google

 ó

¿Has olvidado la contraseña?

No tengo una cuenta, y quiero Registrarme

Escoger idioma y región

English

United States

Polski

Polska

Português

Brasil

English

India

English

Philippines

Español

España

Bahasa Indonesia

Indonesia

Türkçe

Türkiye
How much to ban the user?
1 hour 1 day 100 years