Realiza un mapa conceptual las características de la literatura indígena contemporánea. Asocia éstascon los movimientos étnicos autónomos en México.​

Respuestas 1

Respuesta:

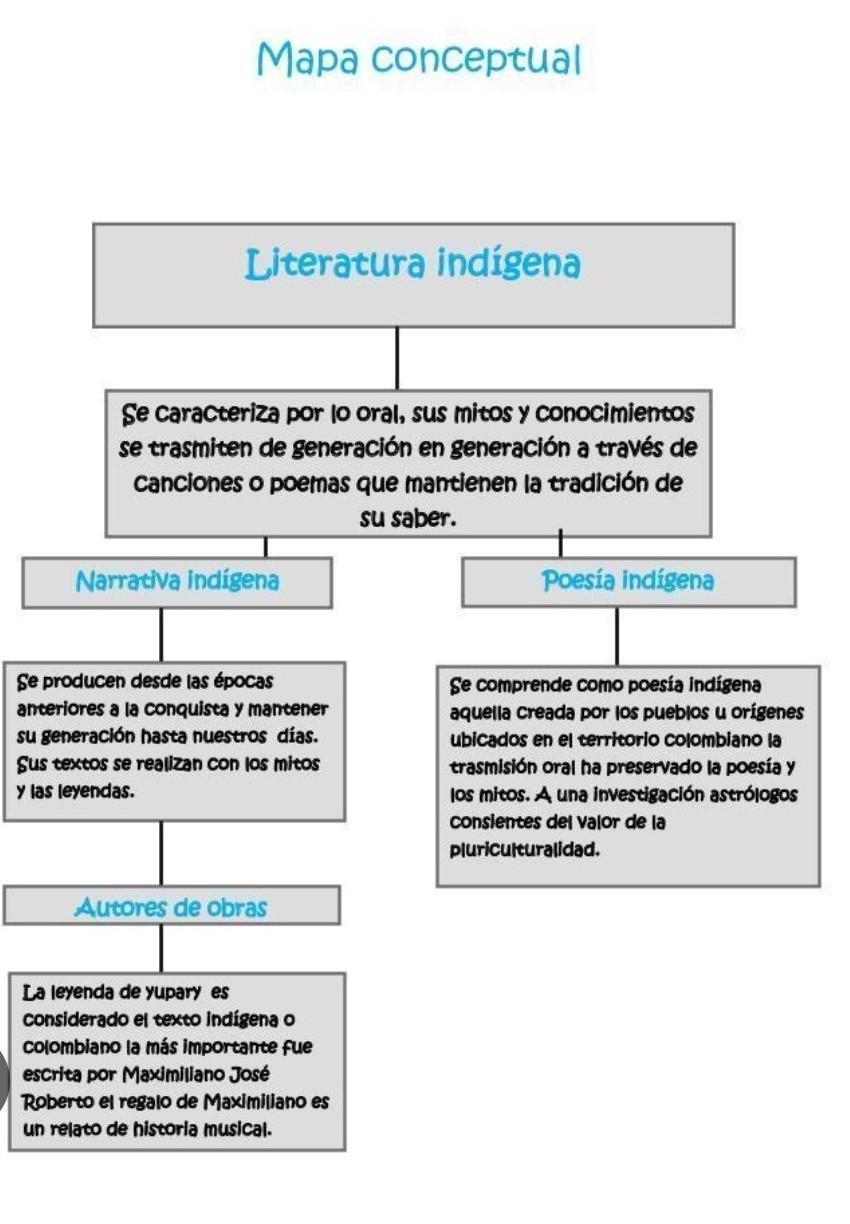
esta dividida en :

literatura indígena

narración indígena

poesía indígena

autores de obras

Explicación:

esto es

espero te sirva

answer img

¿Conoces la respuesta? Añádela aquí

Can't find the answer?

Other related questions that may help you

Mdc de 150 210 240 porfa​

Respuesta:

Para encontrar el máximo común divisor (MCD) de 150, 210 y 240, podemos seguir el método de descomposición en factores primos y luego tomar los factores comunes con la menor potencia. El proceso sería el siguiente:

Primero, descomponemos cada número en factores primos:

150 = 2 * 3 * 5^2

210 = 2 * 3 * 5 * 7

240 = 2^4 * 3 * 5

Luego, identificamos los factores comunes con la menor potencia:

2 aparece en los tres números con exponentes 1, 1 y 4, por lo que lo tomamos con exponente 1.

3 aparece en los tres números con exponentes 1, 1 y 1, por lo que lo tomamos con exponente 1.

5 aparece en los tres números con exponentes 2, 1 y 1, por lo que lo tomamos con exponente 1.

Por lo tanto, el MCD de 150, 210 y 240 es:

MCD(150, 210, 240) = 2^1 * 3^1 * 5^1 = 30

Entonces, el máximo común divisor de 150, 210 y 240 es 30.

Respuesta:

no le hagas caso a lo mal que lo hice

answer img
El hielo seco es un óxido metálico​

Respuesta:

no es un oxido de metálico por que para ser metálico falta

A qué región pertenece el autor que dijo "¿si tenemos puertos por qué depender de Buenos Aires? nosotros podemos cobrar los impuestos y quedarnos con el dinero" ES PARA HOOOY​

Respuesta:

la región mas transparente

en una biblioteca ¿que problemas se resuelven con esta herramienta? (base de datos)​

Respuesta:

Con la base de datos de puede almacenar y ordenar los libros, cuando alguien se lleva prestado uno, cuando lo devuelve y la información precisa de quién lo saco y si lo devolvió o no

Other Filosofía Questions

Iniciar sesión con Google

 ó

¿Has olvidado la contraseña?

No tengo una cuenta, y quiero Registrarme

Escoger idioma y región

English

United States

Polski

Polska

Português

Brasil

English

India

English

Philippines

Español

España

Bahasa Indonesia

Indonesia

Türkçe

Türkiye
How much to ban the user?
1 hour 1 day 100 years