Cualidades en las que trabajará para fortalecer su identidad como abogado.

en la actualidad Honduras cuenta con tres áreas culturales y representativas en su folklore: las danzas criollas las danzas autóctonas y las danzas afro- caribeñas

Yo pienso que tú dibujo está bien, en la forma de la que está el brazo no lo hace ver mal, al contrario lo hace ver más tipo caricaturesco de dibujos animados

Respuesta:

Es la primera lo leí con cuidado y me salió el problema 1

a) La representación del problema a través de un modelo de Programación Lineal es:

\begin{tabular}{r l j k}Calidad & Mina A & Mina B & Extraccion diaria\\Alta & 1 & 2 & 80 \\Media & 3 & 2 & 160 \\Baja & 5&2&200\end{tabular}

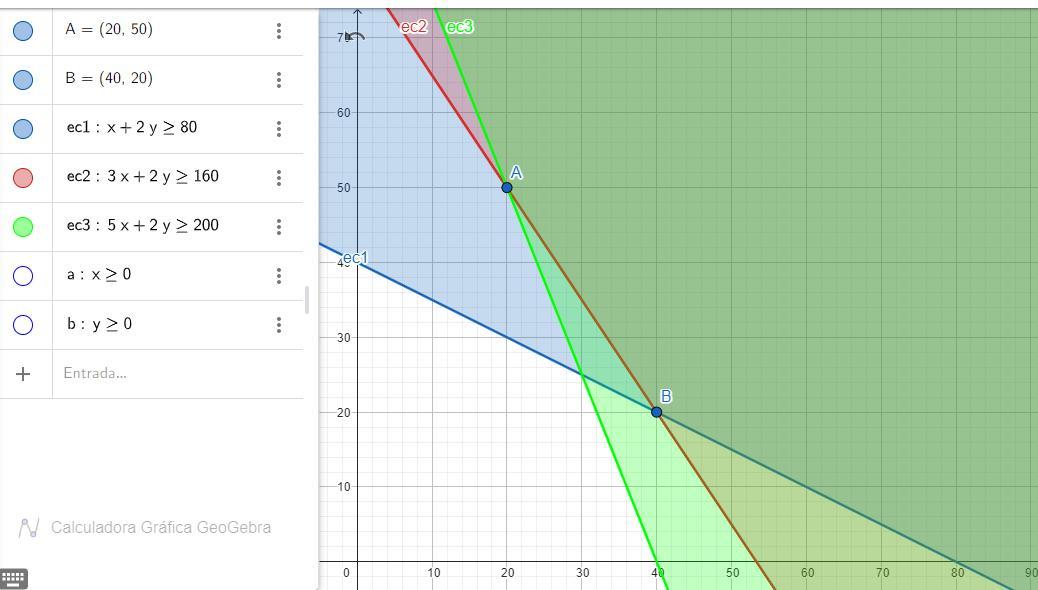
b) La región factible y los vértices para el sistema lineal de dos variables se pueden ver en la imagen adjunta.

c) La cantidad de días que se deberá trabajas en cada mina para obtener el costo total mínimo es:

• Mina A: 40 días
• Mina B: 20 días

El valor mínimo del costo total de extracción de hierro es:

218 millones de dólares

Es un método de optimización matemática que permite establecer un modelo de área en la que se maximiza la ganancia o se reducen los costos.

El método simplex es un método para resolver problemas de programación lineal.

Se puede hacer de forma gráfica, donde la intersección de las ecuaciones que se forman con los datos y restricciones. Se obtiene los puntos de interés a evaluar en la función objetivo.

La función objetivo es que permite maximizar o minimizar.

Definir las variables:

Calidad:   Mina A:    Mina B:   Extracción diaria

Alta             1                2                  80 Ton

Media         3               2                 160 Ton

Baja            5               2                 200 Ton

Restricciones

1. A + 2B ≥ 80
2. 3A + 2B ≥ 160
3. 5A + 2B  ≥ 200
4. x ≥ 0
5. y ≥ 0

Función objetivo

Z = 3.2A + 4.5B

Interceptar las rectas;

Evaluar A(20, 50) en Z;

Z = 3.2(20) + 4.5(50)

Z = 289 millones de dólares

Evaluar B(40, 20) en Z;

Z = 3.2(40) + 4.5(20)

Zmin = 218 millones de dólares

Puedes ver más sobre programación lineal aquí:

https://brainly.lat/tarea/13499147

#SPJ1