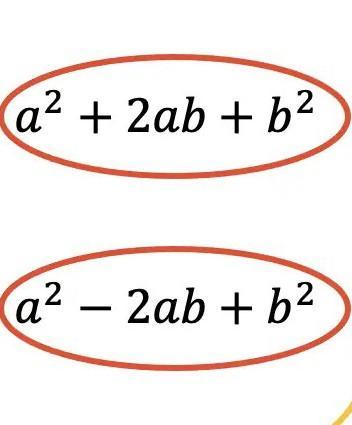que se puede obtener del cobre​

Respuesta:

23/13

Explicación paso a paso:

(4 - 3)³ - (3 - 8)² ÷ (-6+4)² =

(64 - 27) - (9 - 64) ÷ (36 + 16) =

37 - (-55) ÷ 52 =

37 + 55 ÷ 52 =

92 ÷ 52 =

23/13

La solución de esta ecuación es:

(4 - 3)³ - (3 - 8)² ÷ (-6+4)²

1³ - (3 - 8)² ÷ (-6+4)²

1³ - (-5)² ÷ (-6+4)²

1³ - (-5)² ÷ (-2)²

1 - 25 ÷ (-2)²

1 - 25 ÷ 4

1 - 25/ 4

- 21/4

Me das corona pliiiissss

Respuesta:

{(x - 3)}^{2}

Explicación paso a paso:

Se factoriza con la regla del cuadrado perfecto

{(a - b)}^{2} = {a}^{2} - 2ab + {b}^{2}

Para determinar si tienes un trinomio cuadrado perfecto hacemos lo siguiente:

{x}^{2} - 6x + 9 \\ \sqrt{ {x}^{2} } = x \\ \sqrt{9} = 3

Al sacarle la raíz cuadrada nos dan estos valores en el término a (x²) y al termino c (9) al multiplicar esa raíces nos da (3x) y ese 3x se debe de multiplicar por 2 porque el un Trinomio *Cuadrado* Perfecto y debe dar como resultado el término b (6x)

(x)(3) = 3x \\ (3x)(2) = 6x

Entonces si dió por lo que si es un trinomio cuadrado perfecto

Después de eso se debe hacer lo siguiente:

• Con la raíz de x² y 9 ya podemos encontrar la factorización sería haci:

{(x - 3)}^{2}

Esa sería la factorización, El procedimiento fue el siguiente:

• Al sacar la raíz cuadrada de x² queda x, entonces abrimos un paréntesis y ponemos x

• El signo del término b (-6x) en este caso es menos (-) lo ponemos después de la x

• Después sacamos la raíz cuadrada del término c (9) y queda 3 lo ponemos después del signo

• Cerramos paréntesis y elevamos todo eso al cuadrado porque es un Trinomio CUADRADO Perfecto

• Y con eso tienes la solución

Espero te sirva

Respuesta:

ya esta resuelto todos los ejercicios

Respuesta:

Porción material menor de un elemento químico que interviene en las reacciones químicas y posee las propiedades características de dicho elemento

Respuesta:

Los átomos se combinan para formar moléculas que luego interactúan para formar sólidos, líquidos y gases.