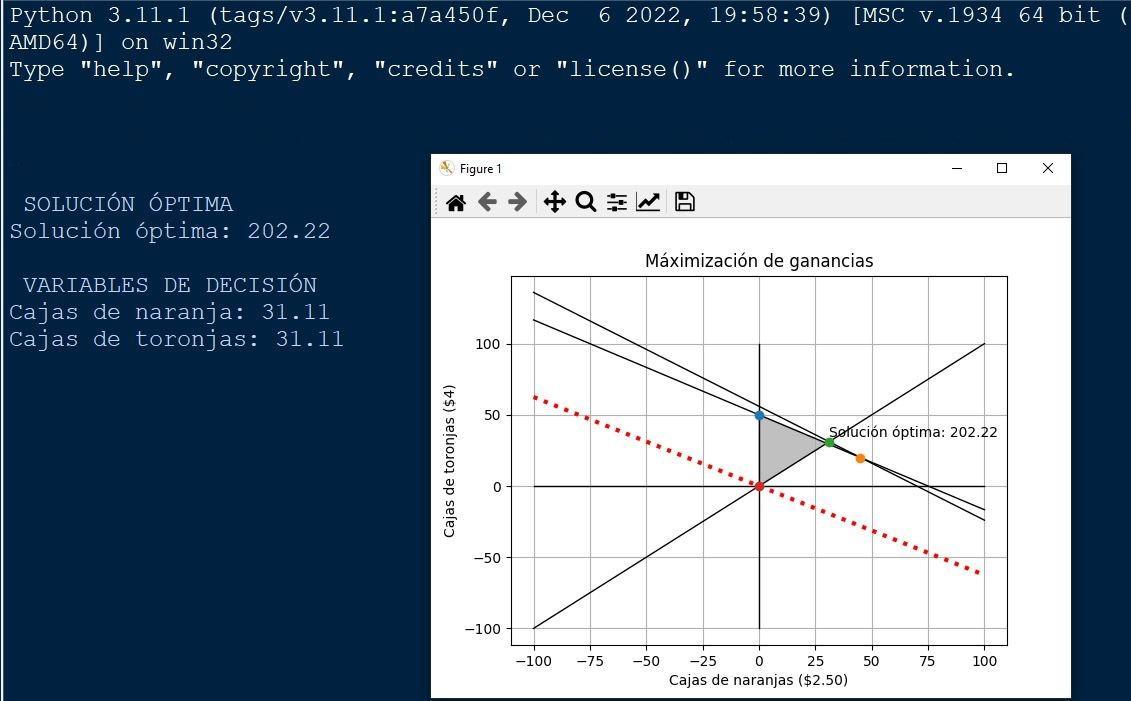
El transportista debe llevar 31 cajas de naranjas y la mísma cantidad de cajas de toronjas a fin de obtener 202.22 dólares de máxima ganancia. A continuación se explica paso a paso el método de solución gráfica.
Variables:
X = Caja de naranjas
Y = Caja de toronjas
Restricciones:
4X + 6Y <= 300
80X + 100Y <= 5600
Y -X <= 0
X >= 0
Y >= 0
Función Objetivo:
MAX (Z) = 2.5X + 4Y
- Paso 2: Pasar las inecuaciones a ecuaciones, despajamos “y”, asignamos un identificador único a y (requisito para la codificación)
4X + 6Y = 300
Y = (300-4X)/6
Y1 = (300-4X)/6
80X + 100Y = 5600
Y = (5600-80X)/100
Y2 = (5600-80X)/100
Y-X = 0
Y = X
Y3 = X
X1 = 0*Y
Y4 = 0*X
Y5 = (-2.5 * X) / 4
- Paso 3: Buscamos la solución optima (mayor ganancia) haciendo iteraciones, para ello utilizamos el método gráfico y el siguiente algoritmo en Python.
Código Python
import matplotlib.pyplot as plt
import numpy as np
from shapely. geometry import LineString
- #Definimos variables con valores de un rango dado
narjas = np.arange(-100, 150, 50)
torjas = np.arange(-100, 150, 50)
- #Representamos restricciones y dibujamos las rectas
y1 = (300-4*narjas)/6
y2 = (5600-(80*narjas))/100
y3 = narjas
x1 = 0 * torjas
y4 = 0 * narjas
y5 = (-2.5 * narjas) / 4
recta1 = LineString(np.column_stack((narjas, y1)))
recta2 = LineString(np.column_stack((narjas, y2)))
recta3 = LineString(np.column_stack((narjas, y3)))
recta4 = LineString(np.column_stack((x1, torjas)))
recta5 = LineString(np.column_stack((narjas, y4)))
recta6 = LineString(np.column_stack((narjas, y5)))
- #Determinamos color y grosor de las líneas
plt.plot(narjas, y1, '-', linewidth=1, color='k')
plt.plot(narjas, y2, '-', linewidth=1, color='k')
plt.plot(narjas, y3, '-', linewidth=1, color='k')
plt.plot(x1, torjas, '-', linewidth=1, color='k')
plt.plot(narjas, y4, '-', linewidth=1, color='k')
plt.plot(narjas, y5, ':', linewidth=3, color='r')
vertic1 = recta4. intersection(recta1)
vertic2 = recta1. intersection(recta2)
vertic3 = recta2. intersection(recta3)
vertic4 = recta3. intersection(recta4)
- #Formateamos la gráfica a mostrar
plt. plot(*vertic1.xy, 'o')
plt. plot(*vertic2.xy, 'o')
plt. plot(*vertic3.xy, 'o')
plt. plot(*vertic4.xy, 'o')
- #Determinamos la solución óptima
vx1, vy1 = vertic1. xy
vx2, vy2 = vertic2. xy
vx3, vy3 = vertic3. xy
vx4, vy4 = vertic4. xy
verticx1 = np. float64(np.array(vx1))
verticx2 = np. float64(np.array(vx2))
verticx3 = np. float64(np.array(vx3))
verticx4 = np. float64(np.array(vx4))
verticy1 = np. float64(np.array(vy1))
verticy2 = np. float64(np.array(vy2))
verticy3 = np. float64(np.array(vy3))
verticy4 = np. float64(np.array(vy4))
- #Evaluando la función objetivo en cada vértice
eval1 = (verticx1 * 2.5) + (verticy1 * 4)
eval2 = (verticx2 * 2.5) + (verticy2 * 4)
eval3 = (verticx3 * 2.5) + (verticy3 * 4)
eval4 = (verticx4 * 2.5) + (verticy4 * 4)
- #Maximizamos los valores obtenidos en la evaluación y mostramos resultados
maximizacion = max(eval1, eval2, eval3, eval4)
maximizacion = round(maximizacion, 2)
print('\n SOLUCIÓN ÓPTIMA')
print('Solución óptima: {}'.format(maximizacion))
- #Ordenando las coordenadas de los vértices y graficamos
m = [verticx1, verticx2, verticx3, verticx4]
n = [verticy1, verticy2, verticy3, verticy4]
plt. fill(m, n, color='silver')
- #Obtenemos el vértice con solución óptima y mostramos las variables
dict1 = {0:eval1, 1:eval2, 2:eval3, 3:eval4}
posicion = max(dict1, key=dict1.get)
xOptimo = round(m[posicion], 2)
yOptimo = round(n[posicion], 2)
print('\n VARIABLES DE DECISIÓN')
print('Cajas de naranja: {} '.format(xOptimo))
print('Cajas de toronjas: {} '.format(yOptimo))
- #Mostramos solución óptima
plt.annotate('Solución óptima: {}'.format(maximizacion), (xOptimo, yOptimo+3))
plt. grid()
plt. xlabel('Cajas de naranjas ($2.50)')
plt. ylabel('Cajas de toronjas ($4)')
plt. title('Máximización de ganancias')
plt. show()
Para saber más acerca máximización por método gráfico consulte https://brainly.lat/tarea/10750144
#SPJ1