ayuda como se resuelve esta inecuacion?
-
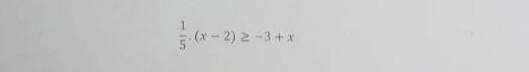
Materia:
Matemáticas -
Autor/a:
guillermo -
Creada:
hace 1 año
Respuestas 2
Respuesta:
La respuesta a esta pregunta es que el valor de x debe ser mayor o igual a 5. Esto se puede determinar mediante la resolución de la ecuación dada. Primero, se debe despejar el término x para obtener una ecuación con un solo término, lo cual se logra restando los dos términos: x-2 >= -3+x. Después de esto, se debe multiplicar ambos lados de la ecuación por -1 para cambiar el signo del lado derecho: -x+2 <= 3-x. Y, por último, se debe sumar los dos términos para obtener el resultado deseado: -x+2+x <= 3-x + x. Esto da como resultado x <= 5, lo que significa que el valor de x debe ser mayor o igual a 5. [1]
-
Autor/a:
perlac2oo
-
Califica una respuesta:
9
\frac{1}{5}(x - 2) \geq -3 + x\\ \\
x - 2 ≥ 5(-3 + x)
x - 2 ≥ -15 + 5x
-5x + x ≥ -15 + 2
-4x ≥ -13 multiplico por -1
4x ≤ 13
x ≤ 13/4
CS = < - ∞ ; 13/4 >
☆༒ Eternamente axllxa ༒☆
-
Autor/a:
bobcole
-
Califica una respuesta:
0
¿Conoces la respuesta? Añádela aquí
Other related questions that may help you
-
Autor/a:
martín52
-
Autor/a:
wolfgangermr
-
Califica una respuesta:
3
-
Autor/a:
godofredo
-
Autor/a:
maddisonp8xz
-
Califica una respuesta:
6
-
Autor/a:
hugh75
-
Autor/a:
silverarcher
-
Califica una respuesta:
1