Sobew un linea se consideran los puntos colineales y consecutivos a, b, c, d y e; tal que: AC=BD; BC=DE/3 y 3/2ab+DE=36 hallar AE
-
Materia:
Matemáticas -
Autor/a:
patel -
Creada:
hace 1 año
Respuestas 1
Respuesta:
AE = 48
Explicación paso a paso:
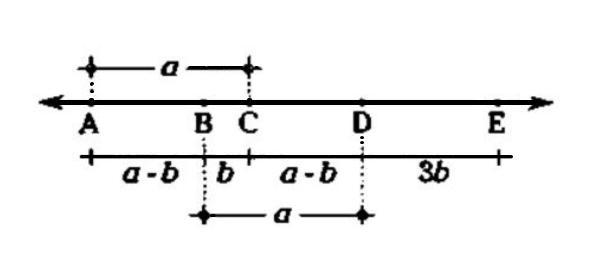
Luego de hacer el gráfico, según las condiciones del problema, reemplazamos sus valores según los datos del problema:
Les ponemos variables a estas igualdades AC = BD = a, BC = b => b = DE/3, 3b = DE
Como AB = a-b y DE = 3b, a la expresión (3AB)/2 + DE = 36 también la podemos representar como 3(a-b)/2 + 3b = 36
Efectuamos esta suma de fracciones (3a - 3b)/2 + 3b = 36 => 3a + 3b = 72
Factorizamos la expresión 3a + 3b = 72 => 3(a+b) = 72, luego simplificamos => a + b = 24
Por ultimo encontramos AE = ?, que también lo podemos representar como AE = AB + a + 3b
Recordamos que AB = a-b y reemplazamos AE = (a-b) + a + 3b => AE = 2a + 2b
Factorizamos la expresión AE = 2a + 2b => AE = 2(a+b), como a + b = 24 reemplazamos AE = 2(24), por lo tanto AE = 48.
-
Autor/a:
pascualhskt
-
Califica una respuesta:
2
