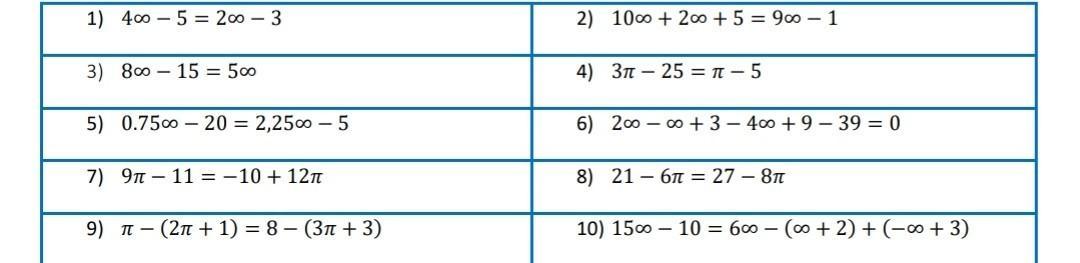
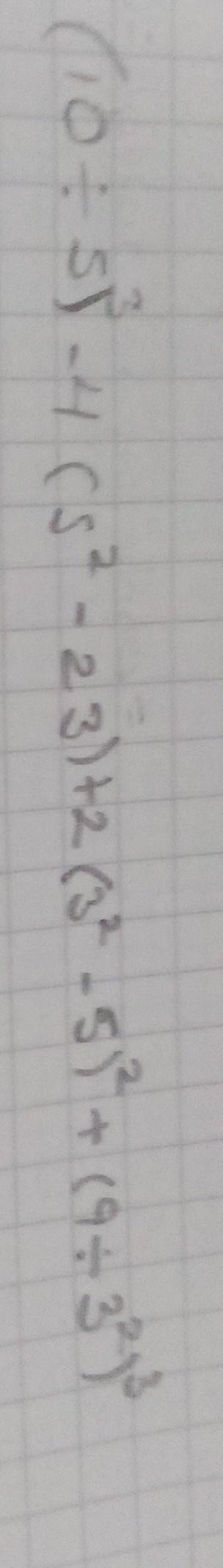Ejercicio 1 Hallar el término de lugar 120 de la progresión aritmética: -8; -3; 2; 7; 12; .... A) 597 D) 582 Ejercicio 2 la P. A: A) 79 3 B) A) - 21 y 2 D) - 19 y 3 Ejercicio 6 31 y 128? 2/3 Nivel I B) 592 E) 587 Hallar el término de lugar 26 de 79 6 A) 3090 D) 3120 * 7 6 ; 5 3 80 6 , C) 577 D) 80 3 Obtener el término a40 en una P. A = 52 y r = - 3 Ejercicio 3 sabiendo que: a25 A) 1 B) 4 C) 7 D) 10 E) 13 Ejercicio 4 Se sabe que en una P. A el término que ocupa el lugar 12 es 42, la razón es 2. E) Hallar el primer término de dicha progresión. A) 24 C) 22 B) 16 D) 18 E) 20 Ejercicio 5 En una P. A el término de lugar 40 es 59; el término de lugar 27 es 33. Hallar el primer tér- mino y la diferencia común de dicha progresión. C) -21 y 3 B) 3100 E) 3130 76 6 B) - 19 y 2 E) - 17 y 2 ¿Cuántos números pares hay entre: A) 45 B) 46 C) 47 D) 48 E) 49 Ejercicio 7 Se desea saber el número de múltiplos de 4 que hay entre 10 y 116. A) 26 B) 27 C) 28 D) 29 E) 30 Ejercicio 8 ¿Cuánto vale la suma de los 25 tér- minos de una P. A, cuyo primer término es 4 y cuya razón es 10? C) 3110 Ejercicio 9 Una P. A de 30 términos tiene por primer término 200 y por suma 5130. ¿Cuánto valen la razón y su último término? A) - 3 y 144 D) - 3 y 142 Ejercicio 10 términos de la P.A. A) 4565 D) 4702 A) 109 B) 110 C) 111 D) 112 E) 113 Ejercicio 11 Hallar la suma de los números im- pares desde 29 hasta 137. A) 39 y 2577 D) 41 y 2583 B) - 2 y 140 C) -2 y 142 E) - 2 y 144 Hallar la suma de los 25 primeros A) 10 y 295 D) 5 y 300 Ejercicio 14 tes a 50. A) 3825 D) 3840 2 5 Ejercicio 12 Hallar el número de términos y la suma de ellos, en una P. A, cuya rázón es 3, su primer término es 6 y su último término 123. C) 39 y 2580 Ejercicio 13 En una progresión aritmética de 60 términos la diferencia común es igual a 5 y la suma de sus términos es 9150. ¿Cuánto vale aj y a60? C) 0 y 305 11 16 ; 15 15 A) (x + 184) D) (x + 179) B) 4594 E) 4428 B) 40 y 2580 E) 40 y 2577 A) 15 B) 6 B) 5 y 305 E) 0 y 295 Sumar los 30 múltiplos de 5 siguien- C) 4536 B) 3830 E) 3 820 Ejercicio 15 Una progresión aritmética tiene 33 términos y su término central vale 8. ¿Cuánto vale la suma de los 33 términos? A) 263 B) 264 C) 265 D) 266 E) 267 Ejercicio 16 En la siguiente: P. A. (x-6); (x-1); (x + 4); (x + 9); Hay 37 términos. Hallar el último término: C) 3835 B) (x + 169) E) (x + 174) "C) (x + 164) Ejercicio 17 El mayor de tres números que for- man una progresión aritmética es el triple del menor. ¿Cuál es el mayor de estos tres números, si su produc- to es 1296? C) 18 D) 12 E) 21​

Respuesta: 1. Se lanzan 20 monedas en las que la probabilidad de cara es de 0,6. Calcular cual es el

número mas probable de caras y qué probabilidad hay de que salga dicho número.

SOLUCIÓN:

El número de caras obtenido al lanzar 20 monedas es una variable aleatoria con distribución

binomial de parámetros B(20;0,6). El número mas probable de caras es

20 ⋅ 0,6 − 0,4 ≤ m ≤ 20 ⋅ 0,6 + 0,6 ⇒11,6 ≤ m ≤ 12,6 . Luego el número mas probable de

caras es 12, y la probabilidad de 12 caras es:

0,0022 0,0007 0,0202

12!8!

20! 0,6 0,4

12

20 ( 12) 12 8 ⋅ ⋅ = ⋅ ⋅ ⋅ = 

 



 P X = =

2. Sabiendo que P(AIB) = 0,6)y que la de la P(AIB =0,2), se pide calcular la

probabilidad de A.

SOLUCIÓN:

P(A)= P[(AIUI B) (A B )]= P(AI I B) + P(A B )=0,6+0,2=0,8

3. Supongamos que las cotizaciones de las acciones de Telefónica y Sniace son variables

aleatorias independientes, y que la probabilidad de que un día cualquiera suban es del

70% para ambas. ¿Cuál es la probabilidad de que un día suba sólo una de ellas?

SOLUCIÓN:

Sea p1 la probabilidad de que suba Telefónica y p2 la de que suba Sniace. La probabilidad de

que solo suba una de ellas será:

p1 (1 - p2) + (1 – p1) p2 = 0,7 0,3 + 0,3 0,7 = 0,21 + 0,21 = 0,42

4. Sean 2 sucesos A y B de los que se sabe que la probabilidad de B es el doble que la de A;

que la probabilidad de su unión es doble que la de su intersección; y que la probabilidad

de su intersección es de 0,1. Se pide: 1) Calcular la probabilidad de A. 2) ¿Qué suceso es

más probable que ocurra sabiendo que ya ha ocurrido el otro?.

SOLUCIÓN:

1) Sea P(A) = x; entonces: P(B)= 2X. Además P[AUB] = 0,2 y P[AIB] = 0,1

P[AUB] = P(A)+P(B)- P (AIB))=x+2x-0,1=3x-0,1

P[AUB] = 3x – 0,1=0,2. despejando x=1

Por tanto P(A) = 0,1 y P(B) = 0,2.

2) Las probabilidades condicionadas serían:

P(A/B)= 0,5; 0,2

0,1

( )

( )

= = P B

P AIB

P(B/A)= 1

0,1

0,1

( )

( )

= = P A

P AIB

Por tanto es más probable que ocurra B sabiendo que ha ocurrido A, que, que ocurra A sabiendo

que ha ocurrido B.

5. La probabilidad de cara de dos monedas son 0,4 y 0,7. Calcular la probabilidad de que

al lanzar las dos monedas salga sólo una cara. Repetir el ejercicio considerando que las

monedas están bien construidas.

SOLUCIÓN:

Para que salga solo una cara ha de ocurrir una de las dos cosas siguientes: que la primera

moneda saque cara y la segunda cruz o viceversa:

P[(C I X ) U (XIC)] = 0,4⋅ 0,3 + 0,6 ⋅ 0,7 = 0,12 + 0,42 = 0,54

Si las monedas están bien construidas las probabilidades de cara y cruz son iguales a 0,5; por

tanto: P[(C I X ) U (XIC)] = 0,5⋅ 0,5 + 0,5⋅ 0,5 = 0,5

6. Dos maquinas A y B han producido respectivamente, 100 y 200 piezas. Se sabe que A

produce un 5% de piezas defectuosas y B un 6%. Se toma una pieza y se pide:

1) Probabilidad de que sea defectuosa.

2) Sabiendo que es defectuosa, probabilidad de que proceda de la primera máquina.

SOLUCIÓN:

Indiquemos por: MA = {la pieza procede de la maquina A}

MB = {la pieza procede de la maquina B}

Entonces Ω = {300 piezas} = MA + MB

3

1 Ρ(ΜΑ ) = 3

2 Ρ(ΜΒ ) =

1) Sea D = {la pieza defectuosa}

0,0567

3

2 (0,06) 3

1 Ρ(D) = P(D / M A )⋅ P(M A ) + P(D / M B )⋅ P(M B ) = (0,05)⋅ + ⋅ =

2) Es la probabilidad de MA condicionada a la presencia de D

0,2941

0,0567

3

1 (0,05)

( / ) ( ) ( / ) ( )

( / ) ( ) ( / ) =

⋅

= ⋅ + ⋅

⋅ =

A A B B

A A

A P D M P M P D M P M

P D M P M P M D

7. Sea la urna U (2B, 3N, 4R). Extraemos tres bolas, una a continuación de la otra. La

primera es negra, la segunda no se mira y la tercera es blanca. Hallar la probabilidad de

que la segunda sea roja.

SOLUCIÓN:

Una vez es extraída la primera bola que es negra, la urna es U(2B, 2N, 4R). Al extraer la

segunda, pueden ocurrir tres casos: que sea blanca, negra o roja, obteniéndose tres urnas

distintas, con probabilidad 1/4, 1/4 y 1/2 respectivamente. La tercera bola procede de una de

estas tres posibles urnas.