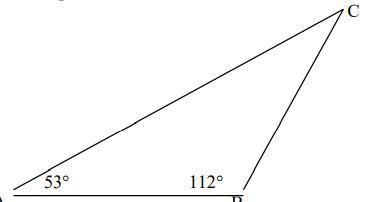
Sandra Catalina se encuentra en el punto A y desea visitar a su novio Jonathan que se encuentra en el punto C a 2.8 kms en línea recta. Debido a que el terreno está en malas condiciones, decide seguir la trayectoria de A a B para dirigirse finalmente a C. ¿Cuál es la distancia total que deberá recorrer?
-
Materia:
Matemáticas -
Autor/a:
jonroth -
Creada:
hace 1 año
Respuestas 1
Respuesta:
Primero se obtiene la medida del ángulo C, para luego aplicar la ley de senos.
∡A = 53º, ∡B = 112º ⇒ ∡A + ∡B + ∡C = 180º
⇒ 53º + 112º + ∡C = 180º ⇒ 165º + ∡C = 180º ⇒ ∡C = 15º
Como \mathbf{\overline{AC}=2.8\ km}, entonces utilizando la ley de senos se tendría:
\mathbf{\frac{\overline{AB}}{senC} =\frac{\overline{AC}}{senB} \ \Rightarrow \overline{AB}=(senC)(\frac{\overline{AC}}{senB})}\\\\\mathbf{\Rightarrow \overline{AB}=(sen15\º)(\frac{2.8}{sen112\º})\ \Rightarrow \underline{\overline{AB}=0.78\ km}}
Por otro lado:
\mathbf{\frac{\overline{BC}}{senA} =\frac{\overline{AC}}{senB} \ \Rightarrow \overline{BC}=(senA)(\frac{\overline{AC}}{senB})}\\\\\mathbf{\Rightarrow \overline{BC}=(sen53\º)(\frac{2.8}{sen112\º})\ \Rightarrow \underline{\overline{BC}=2.41\ km}}
Por lo tanto la distancia total recorrida será: 0.78 + 2.41 = 3.19 km
-
Autor/a:
plutoqumu
-
Califica una respuesta:
4
¿Conoces la respuesta? Añádela aquí
Other related questions that may help you
-
Autor/a:
janetta
-
Autor/a:
bunny rabbithkco
-
Califica una respuesta:
9
-
Autor/a:
larson
-
Autor/a:
rosietoql
-
Califica una respuesta:
9
