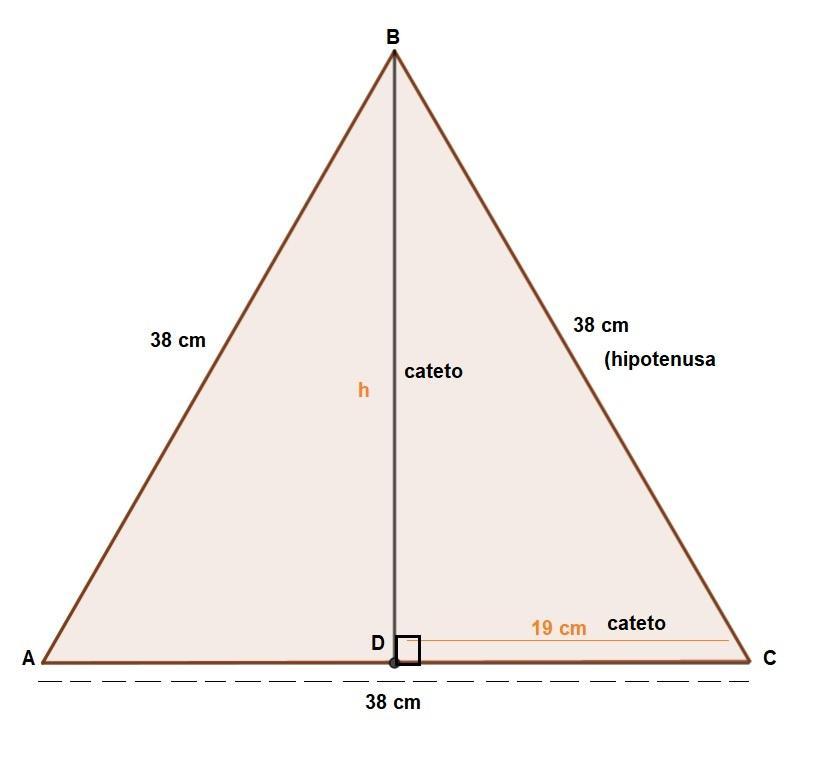
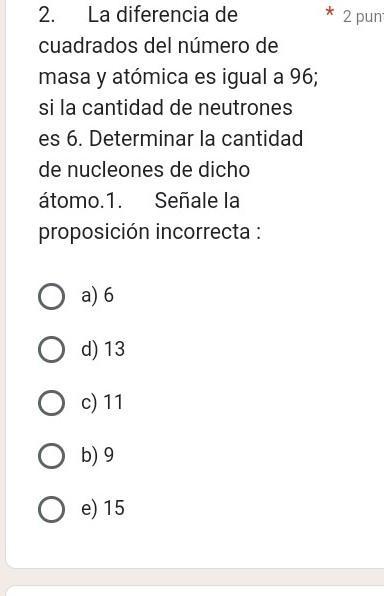
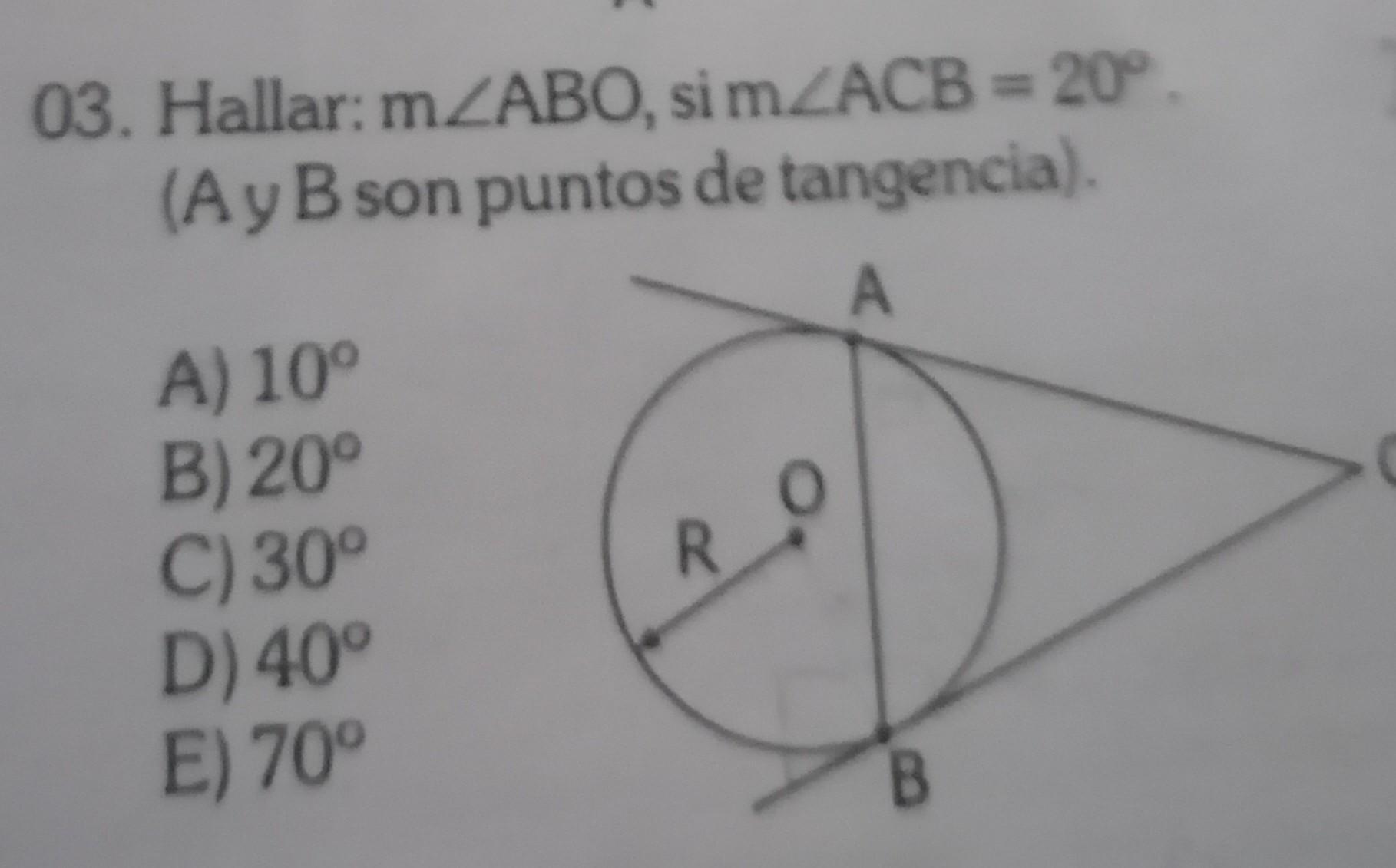
Ayuda Hallar: m/ABO, si m/ACB= 20°. (A y B son puntos de tangencia).
-
Materia:
Matemáticas -
Autor/a:
jordon91 -
Creada:
hace 1 año
Respuestas 1
Respuesta:
puedes usar el transportador
-
Autor/a:
bellavmer
-
Califica una respuesta:
4
¿Conoces la respuesta? Añádela aquí
Other related questions that may help you
-
Autor/a:
dexter35
Respuesta:
La altura mide 32,9 cm
Explicación paso a paso:
Si la base (que es uno de los lados) mide 38 cm, entonces los otros dos lados también miden cada uno, 38 cm, porque el triángulo es equilátero.
El dato que el ejercicio da sobre el área, es incorrecto, porque:
A=\frac{\sqrt{3}*l^{2}}{4}=\frac{\sqrt{3}*38^{2}}{4}=625,27cm^{2} O sea que el área son 625,27 cm2 y no 160cm2
Calculemos la altura. Mira la imagen adjunta:
La altura (h) es perpendicular a la base y forma con está un ángulo recto, además, por propiedad, esa altura divide a la base en dos partes iguales. Entonces se forma el triángulo rectángulo CDB, que ves en la imagen adjunta, cuya hipotenusa mide 38 cm, su base es el cateto menor, que mide 19 cm (o sea la mitad de 38) y el otro cateto es la altura que hemos denominado h.
Aplicamos T de Pitágoras para despejar h: 38^{2}=h^{2}+19^{2}
h^{2}=38^{2}-19^{2} ∴ h=\sqrt{38^{2}-19^{2}} ∴ h=32,9cm
-
Autor/a:
silverarcher
-
Califica una respuesta:
2
-
Autor/a:
jazminberry
-
Autor/a:
taylorsrhu
-
Califica una respuesta:
1