DOY CORONA, SOLO SI TIENE EL DESARROLLO COMPLETO
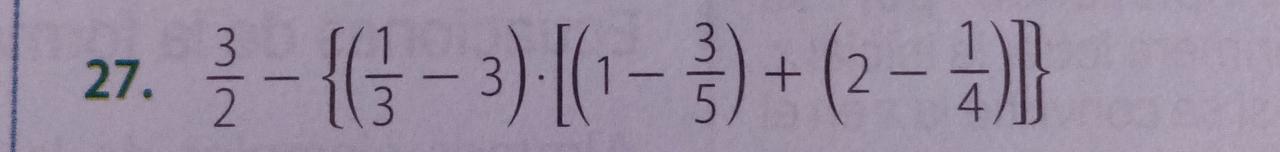
-
Materia:
Matemáticas -
Autor/a:
jerónimo -
Creada:
hace 1 año
Respuestas 2
Soy de 4to de secundaria... no sé si este proceso es el que necesitas, espero que si. También espero que te sirva y este bien.

-
Autor/a:
emilio120
-
Califica una respuesta:
1
Fracciones HOMOgeneas :v
Son las fracciones que tienen el mismo denominador.
estas fracciones tienen la facultad que en sumas y restas , el resultado mantiene el mismo denominador ,pero los numeradores se suman o restan dependiendo del caso.
Ejemplo :
\frac{1}{3} + \frac{4}{3} = \frac{1+4}{3} = \frac{5}{3}
Guiándonos de este método resolveremos el problema:
27.- \frac{3}{2} - ((\frac{1}{3}-3).[(1-\frac{3}{5})+(2-\frac{1}{4})])
Procedemos desarrollando el contenido de los parentesis.
(1-\frac{3}{5} )= \frac{5}{5} - \frac{3}{5} = \frac{2}{5} (el "1" lo transformé en su equivalente 5/5 para poder realizar una resta de fracciones homogeneas)
(2-\frac{1}{4}) = \frac{8}{4} - \frac{1}{4} = \frac{7}{4} (aqui hice lo mismo que en el anterior ejemplo,
(\frac{1}{3}-3) = \frac{1}{3} - \frac{3}{3} = \frac{-2}{3}
Ahora reemplazemos esos valores en el problema principal:
\frac{3}{2} - ((-\frac{2}{3}).[(\frac{2}{5})+(\frac{3}{4})])
Procedemos a operar ahora de la misma manera lo que esta dentro de los paréntesis.
\frac{2}{5} + \frac{3}{4} = \frac{8}{20} + \frac{15}{20} = \frac{23}{20}
este nuevo resultado lo reemplazamos en el problema original.
\frac{3}{2} - ((-\frac{2}{3}).[\frac{23}{20}])
Ahora procedemos a multiplicar fracciones:
regla general:
\frac{a}{b} . \frac{X}{Y} = \frac{a.X}{b.Y}
Aplicando esa regla:
\frac{-2}{3}.\frac{23}{20} = \frac{-46}{60}
esto lo reemplazamos en el problema original.
\frac{3}{2} - (\frac{-46}{60})
Ahora finalmente hacemos lo mismo:
\frac{3}{2} - (\frac{-46}{60}) = \frac{90}{60} + \frac{46}{60} = \frac{136}{60}
Ley de signos :
menos por menos = positivo ( - . - = + )
Espero haberte ayudado.
-
Autor/a:
treyll6n
-
Califica una respuesta:
5
