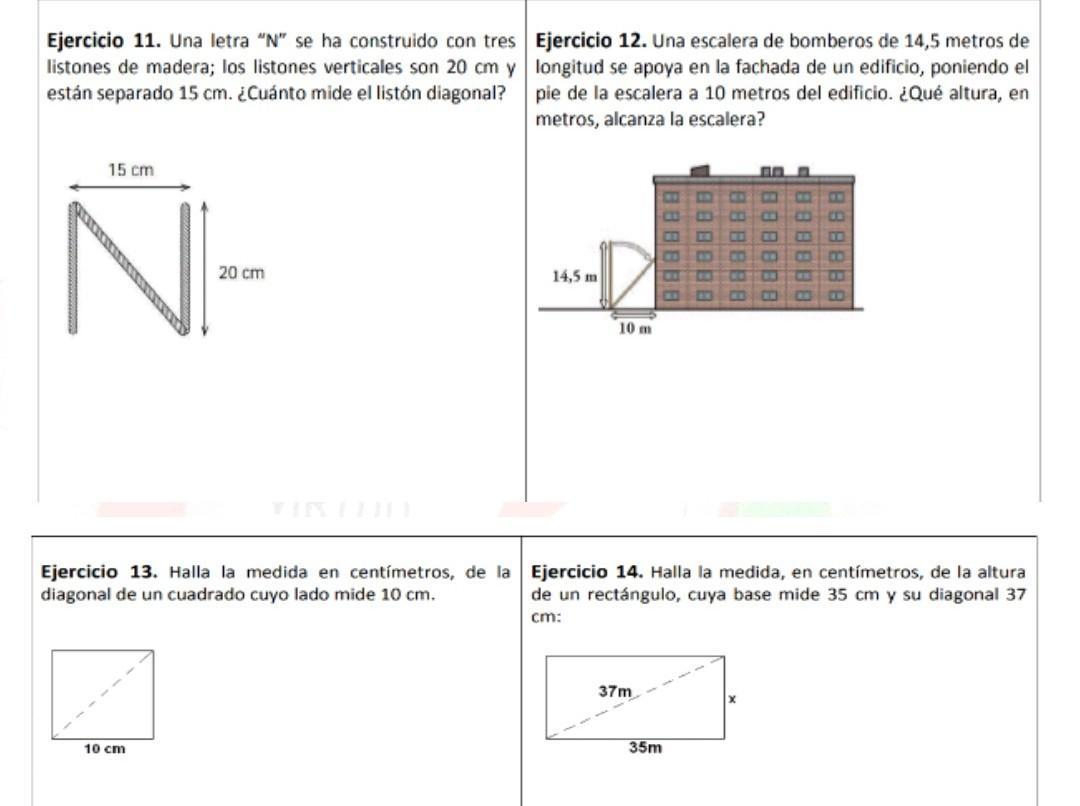
Ejercicio 11. Una letra "N" se ha construido con tres listones de madera; los listones verticales son 20 cm y están separado 15 cm. ¿Cuánto mide el listón diagonal?
El listón diagonal mide aproximadamente 25 cm. Esto se calcula usando la fórmula de la hipotenusa de un triángulo rectángulo: c = raiz cuadrada de (a^2 + b^2), donde a y b son los lados opuestos y c es la hipotenusa. En este caso, a = 15 cm y b = 20 cm, lo que da c = raiz cuadrada de (15^2 + 20^2) = 25 cm.
Ejercicio 12. Una escalera de bomberos de 14,5 metros de longitud se apoya en la fachada de un edificio, poniendo el pie de la escalera a 10 metros del edificio. ¿Qué altura, en metros, alcanza la escalera?
La altura a la que alcanza la escalera es de 4,5 metros. Esto se calcula restando la longitud de la escalera (14,5 metros) a la distancia del edificio desde el pie de la escalera (10 metros).
Ejercicio 13. Halla la medida, en centímetros, de la altura diagonal de un cuadrado cuyo lado mide 10 cm.
La medida de la altura diagonal de un cuadrado de 10 cm. de lado es de 14.14 cm.
El procedimiento para calcular la altura diagonal de un cuadrado consiste en usar la fórmula:
Diagonal = Raíz cuadrada de (lado al cuadrado + lado al cuadrado)
En este caso, la fórmula aplica de la siguiente forma:
Diagonal = Raíz cuadrada de (10 cm al cuadrado + 10 cm al cuadrado)
Diagonal = Raíz cuadrada de (100 cm al cuadrado + 100 cm al cuadrado)
Diagonal = Raíz cuadrada de (200 cm al cuadrado)
Diagonal = Raíz cuadrada de 200 cm al cuadrado
Diagonal = 14.14 cm
Por lo tanto, la medida de la altura diagonal de un cuadrado de 10 cm. de lado es de 14.14 cm.
Ejercicio 14. Halla la medida, en centímetros, de la altura de un rectángulo, cuya base mide 35 cm y su diagonal 37 cm:
La altura de un rectángulo se puede calcular utilizando la ecuación a²+b²=c², donde a y b son los lados del rectángulo y c es la diagonal. Por lo tanto, reemplazando los valores conocidos, tenemos:
35² + h² = 37²
1225 + h² = 1369
h² = 144
h = √144
h = 12 cm
Por lo tanto, la altura del rectángulo es de 12 cm.