Ayuda con las operaciones de mates
-
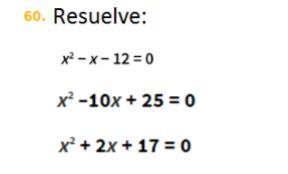
Materia:
Matemáticas -
Autor/a:
snickers -
Creada:
hace 1 año
Respuestas 1
{x}^{2} - x - 12 = 0 \\ \\ \frac{ - ( - 1) + - \sqrt{ {( -1)}^{2} - 4(1 \times ( - 12) )} }{2(1)} = x \\ \frac{1 + - \sqrt{1 + 48} }{2} = x \\ x = \frac{1 + 7}{2} = 4 \\ x = \frac{1 - 7}{2} = - 3
{x}^{2} - 10x + 25 = 0 \\ \\ \frac{ - ( - 10) + - \sqrt{ {( - 10)}^{2} - 4(1 \times 25) } }{2(1)} = x \\ \frac{10 + - \sqrt{100 - 100} }{2} = x \\ x = \frac{10 + - 0}{2} = 5
{x}^{2} + 2x + 17 = 0 \\ \\ \frac{ - 2 + - \sqrt{ {2}^{2} - 4(1 \times 17) } }{2(1)} = x \\ \frac{ - 2 + - \sqrt{4 - 68} }{2} = x \\ \sqrt{ - 64} = sin \: solucion
2( {x}^{2} - 10x) = 33 - x \\ {2x}^{2} - 20x = 33 - x \\ 2 {x}^{2} - 19x - 33 = 0 \\ \\ \frac{ - ( - 19) + - \sqrt{ {( - 19)}^{2} - 4(2 \times - 33) } }{2(2)} = x \\ \frac{19 + - \sqrt{361 - ( - 264)} }{4} = x \\ \frac{19 + - \sqrt{625} }{4} = x \\ x = \frac{19 + 25}{4} = 11 \\ x = \frac{19 - 25}{4} = - \frac{3}{2}
4( {x}^{2} - 3x + 4) = - (5{x}^{2} + 6x + 1) \\ 4 {x}^{2} - 12x +16 = - 5 {x}^{2} - 6x - 1 \\ 9 {x}^{2} - 6x + 17 = 0 \\ \\ \frac{ - ( - 6) + - \sqrt{ {( - 6)}^{2} - 4(9 \times 17)} }{2(9)} = x \\ \frac{6 + - \sqrt{36 - (36 \times 17) } }{18} = x \\ x = sin \: solucion
3 {x}^{2} + 4x + 12 = 2 {x}^{2} + 4x + 37 \\ {x}^{2} + 0x - 25 = 0 \\ \\ \frac{ - 0 + - \sqrt{ {0}^{2} - 4(1 \times - 25) } }{2(1)} = x \\ \frac{0 + - \sqrt{0 - ( - 100)} }{2} = x \\ x = \frac{ 0 + 10}{2} = 5 \\ x = \frac{0 - 10}{2} = - 5
-
Autor/a:
tobiasbk8n
-
Califica una respuesta:
11
¿Conoces la respuesta? Añádela aquí
Other related questions that may help you
-
Autor/a:
deshawnrosales
-
Autor/a:
foxsuws
-
Califica una respuesta:
6
-
Autor/a:
iliana
-
Autor/a:
encarnaciónmgst
-
Califica una respuesta:
2
-
Autor/a:
amadeo
-
Autor/a:
geniusgg40
-
Califica una respuesta:
6
-
Autor/a:
porfiriose9u
-
Califica una respuesta:
7