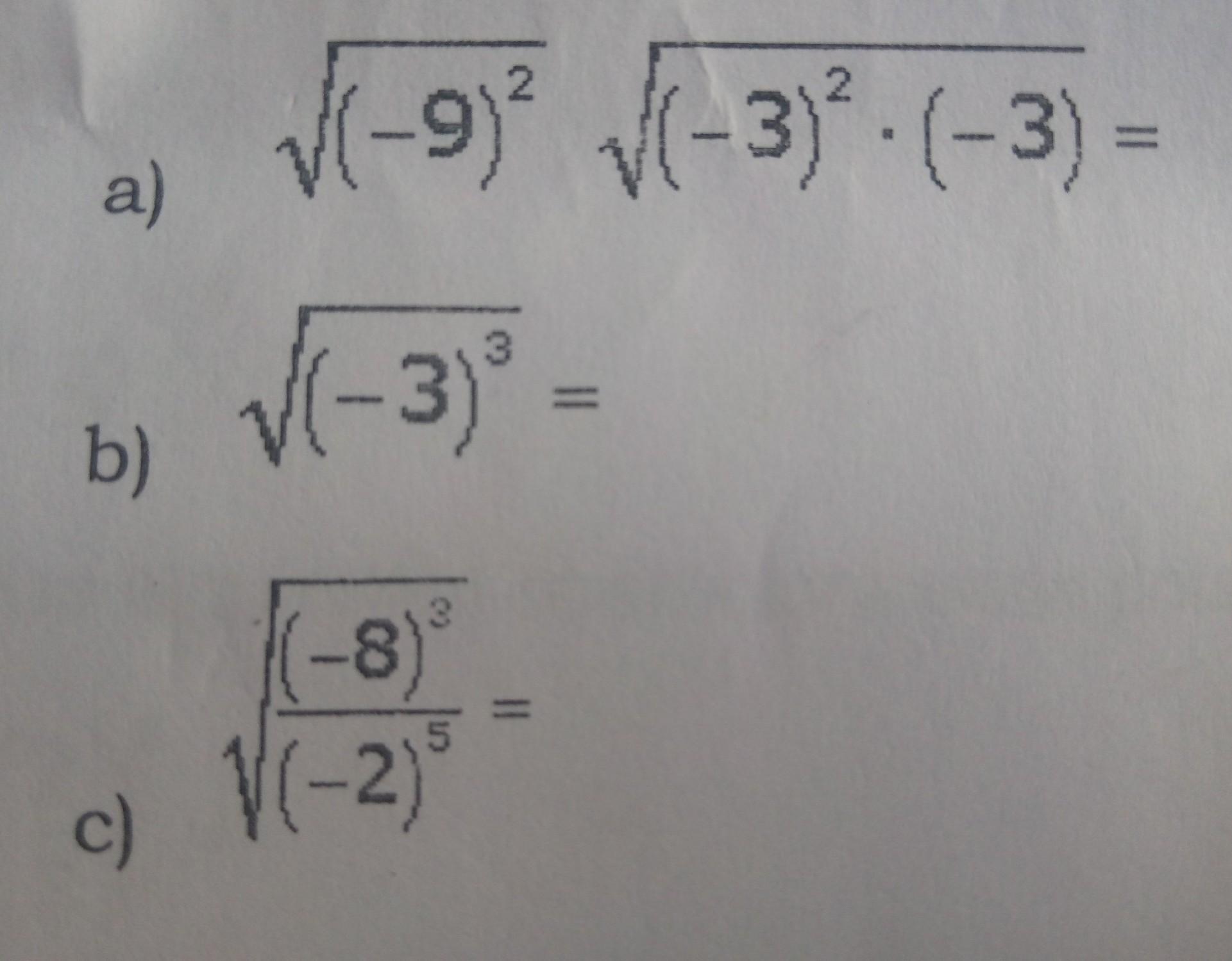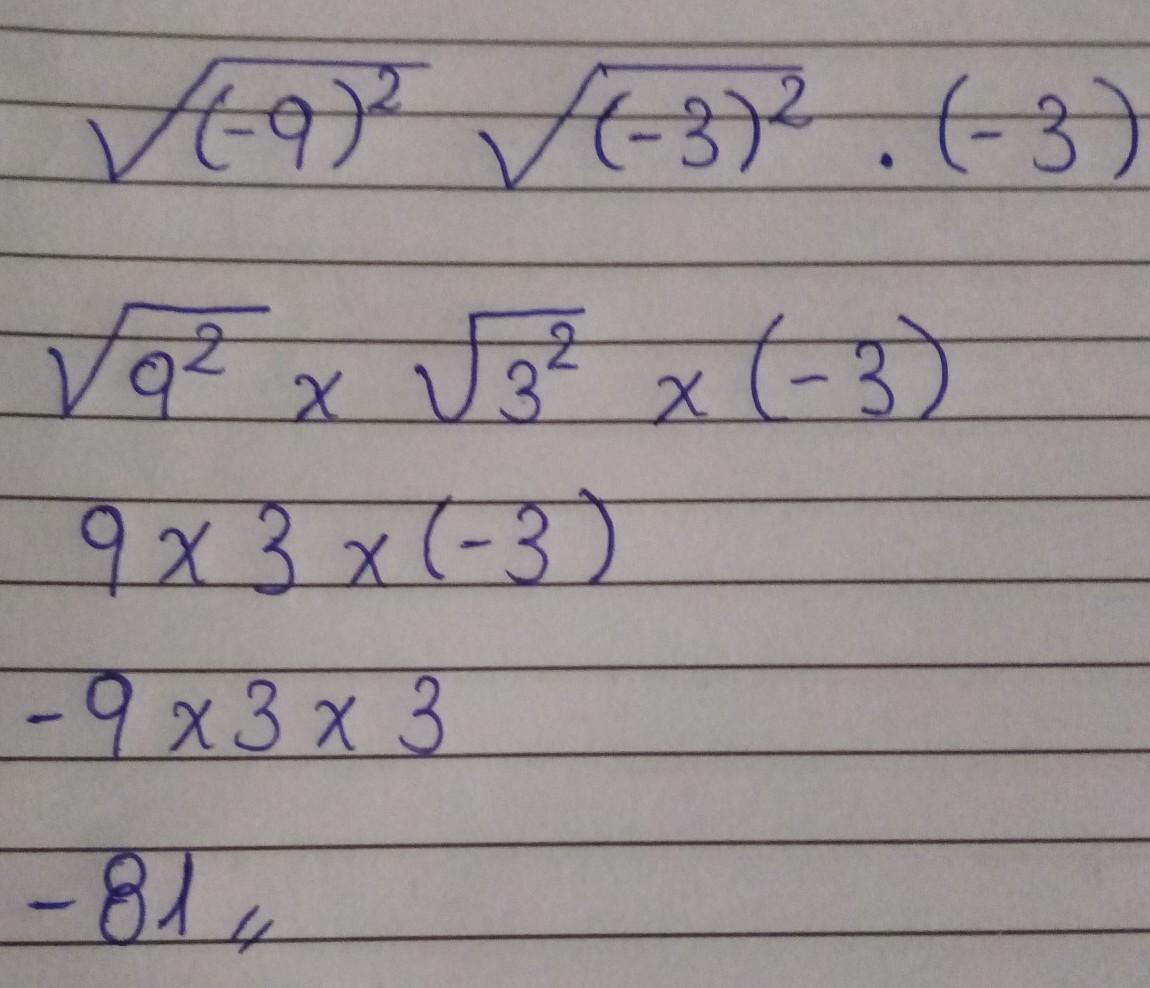la suma de un numero con su posterior y su anterior es 147 ¿cuales son los numeros

Respuesta:

---En el cuento "Algo muy grave va a suceder en este pueblo", se puede notar que originalmente la historia fue relatada de forma oral debido a la estructura narrativa del cuento, la cual está compuesta por una serie de escenas narradas con un lenguaje poético, metaforas, imágenes alegóricas y diálogos que reflejan la cultura y el folclore local. Además, la narración se hace a través de personajes principales y secundarios, cuyas situaciones y acciones están relacionadas entre sí y conducen hacia un desenlace trágico. Estos elementos son característicos del relato oral, lo que sugiere que el cuento fue transmitido de forma oral antes de ser escrito.---

:⁠-⁠P

Explicación:

Salu2!!! ✔

Respuesta:

a) El valor de la fuerza F1 ejercida sobre q1 por q2 es de 9.6 x 10⁹ N.

a) El valor de la fuerza F1 ejercida sobre q1 por q2 es de 9.6 x 10⁹ N. b) El valor de la fuerza ejercida sobre q2 por q1 es igual a F1.

a) El valor de la fuerza F1 ejercida sobre q1 por q2 es de 9.6 x 10⁹ N. b) El valor de la fuerza ejercida sobre q2 por q1 es igual a F1. c) Si las cargas estuvieran sumergidas en el agua, la fuerza eléctrica entre ellas sería menor que si estuvieran en el aire, ya que el agua es un medio conductor. La fuerza eléctrica entre las cargas sería de 5.76 x 10⁹ N.

Pregúntame lo que sea...

Explicación:

Salu2!!! ✔

Respuesta:

a) F_{1} = -0.0225 \ N

b) El valor de la fuerza ejercida sobre q2 por q1 es igual a F1.

c) F = -2.487*10^{-5} N

Explicación:

La primera carga es q1 = 5 μC.

La segunda carga es q2 = -2 μC.

La distancia entre las cargas es r = 200 cm = 2 m.

La ley de Coulomb se expresa como,

F_{1} = k \frac{q_{1} q_{2}}{r^{2} } …(1)

k es la constante de Coulomb.

k = 8.99*10^9\ N.m^{2} /C^2

(a) Determinación de la fuerza F1:

Sustituimos todos los valores conocidos en la ecuación (1), y obtenemos,

F_{1} = 8.99*10^9\ N.m^{2} /C^2 * \frac{5\mu C * -2\mu C}{(2m)^{2} }

F_{1} = 8.99*10^9\ N.m^{2} /C^2 * \frac{5*10^{-6} C * (-2*10^{-6} C)}{(2m)^{2} }

F_{1} = -0.0225 \ N

(b) El valor de la fuerza ejercida sobre q2 por q1 igual o diferente de F1:

De la ecuación (1),

La expresión de la fuerza se expresa como,

F_{2} = k \frac{q_{2} q_{1}}{r^{2} }...(2)

De las ecuaciones (1) y (2),

La magnitud de las fuerzas es igual, es decir,

F_{1} = F_{2}

Entonces, el valor de la fuerza ejercida sobre q2 por q1 es igual a F1.

(c) Determinación de la fuerza eléctrica entre las cargas si estuvieran sumergidas en agua

La fuerza eléctrica entre las cargas si estuvieran sumergidas en agua se expresa como,

F = \frac{1}{4\pi e} \frac{q_{1} q_{2}}{r^{2} }...(3)

donde e es la permitividad del agua.

El valor de la permitividad del agua es e = 80.

Sustituimos todos los valores conocidos en la ecuación (3) y obtenemos,

F = \frac{1}{4\pi *80} * \frac{5\mu C*(-2\,u C)}{(2m^{2})}

F = \frac{1}{4\pi *80} * \frac{5*10^{-6} C*(-2*10^{-6} C)}{(2m)^{2}}

F = -2.487*10^{-5} N

Respuesta:

El recurso literario más abundante es la antítesis, dado que toda la composición trata de la doble naturaleza positiva y negativa de la Belleza ("cielo/abismo", "infernal/divina", "favores/crimen", "aurora/ocaso", "envalentonan/acobardan...).

Explicación paso a paso:

De la misma forma es el ejercicio b y c, espero haberte ayudado.