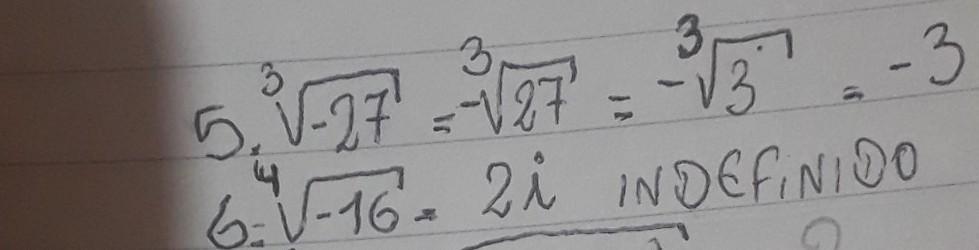Aportes max Weber a la religión y durkheim

Respuesta:

oscuridad-luminosidad

friolero-caluroso

agilidad-lentitud

sensibilidad-insensibilidad

capacidad-incapacidad

graveza-delicadeza

Explicación:

espero haberte ayudado

como la esposa,la hija ,el hijo, el payaso,el homero , el vecino

Tema: Exponentes y raíces

\boxed{\sqrt[3]{-27}=-3}

\boxed{\sqrt[4]{-16}=2i}

Desarrollo:

Tus respuestas están correctas, con gusto te ayudo repasar para comprender mejor el tema. Cabe aclarar que lo siguiente es la forma en que yo lo haría, sin embargo puedes hacerlo de otra manera siempre y cuando tus procedimientos sean correctos :)

Primera operación:

\sqrt[3]{-27}

Lo primero, será descomponer el número 27 en factores primos, nos quedaría de la siguiente forma:

27=3 \times 3 \times 3

No olvidemos el signo negativo, que podemos obtener multiplicando por -1, entonces nos queda:

\sqrt[3]{-1\times 3 \times 3 \times 3} = \sqrt[3]{-1 \times 3^3}

Ahora aplicaremos las siguientes dos propiedad de la raíz.

La primera propiedad es

\sqrt[n]{a\times b}=(\sqrt[n]{a})(\sqrt[n]{b})  

con lo que nos queda:

\sqrt[3]{-1 \times 3^3}= (\sqrt[3]{-1})(\sqrt[3]{3^3})

En los números reales, cuando tenemos raíces pares, no podemos "sacar" el -1 de la raíz, pero cuando son impares sí, por lo tanto nos queda:

\sqrt[3]{-1})(\sqrt[3]{3^3})=-1(\sqrt[3]{3^3})= -\sqrt[3]{3^3}

La segunda propiedad es:

\sqrt[n]{a^m}= a^{\frac{m}{n} }

Que podemos aplicar como sigue:

-\sqrt[3]{3^3}=-3^\frac{3}{3}

Resolvemos la fracción:

-3^{\not{\frac{3}{3}}}= -3

Con lo que tenemos que: \sqrt[3]{-27}=-3

Segunda operación:

\sqrt[4]{-16}

Entonces, primero descomponemos:

\sqrt[4]{-1 \times 2 \times 2 \times 2 \times 2}= \sqrt[4]{-1 \times 2^4}

Aplicamos la primera propiedad:

\sqrt[4]{-1 \times 2^4}= (\sqrt[4]{-1}) (\sqrt[4]{2^4})

En este caso no podremos sacar el -1 ya que tenemos una raíz par, aplicaremos la propiedad dos a la raíz que contiene el 2:

(\sqrt[4]{-1}) (\sqrt[4]{2^4})=(\sqrt[4]{-1}) (2^{\not{{\frac{4}{4}}}} )=2\sqrt[4]{-1}

Podemos expresar la respuesta en el campo de los números complejos, que es justo como lo hiciste tú:

\sqrt[4]{-1} =i, con lo que tenemos que la respuesta es 2i

¡Saludos!

https://brainly.lat/tarea/13437177

Respuesta:

Perímetro= 50cm

Área=

300cm {}^{2}

Explicación paso a paso:

Área de un pentagono=

\frac{perimetro \: \times \: apotema}{2}

Entonces

10 \times 5 = 50

\frac{50cm \times 12cm}{2} = 300cm ^{2}