con que nombre se la conoce a la persona que dirige la danza del betskate​.matachin menor.matachin mayor.matachin alto mando.todaa las anteriores

Respuesta:

Explicación:

serian 75 por que subio a 95 y ya pesaba 20 asi que solo a 95 le quitamos 20 y serian 74

Respuesta:

En conclusión, el oído es un sistema complejo y sofisticado que permite a los seres humanos percibir y procesar sonidos. Desde el oído externo hasta el oído interno, cada parte desempeña un papel crucial en la transmisión y procesamiento de las señales sonoras. La cóclea es el componente clave del oído interno, y su estructura única permite la transformación de las señales sonoras en impulsos nerviosos que se transmiten al cerebro. Es importante cuidar nuestro oído y protegerlo de los daños por ruido para mantener nuestra capacidad auditiva y disfrutar de la música y los sonidos de nuestro entorno. En general, la anatomía del oído es un ejemplo sorprendente de la ingeniería biológica y la capacidad del cuerpo humano para percibir y procesar el sonido.

Respuesta:opino  que no tengo ni idea pero si lo se te aviso

Explicación:

Respuesta:

a) se requieren 473.700 metros cuadrados de malla

b) el costo total de la malla requerida es $64'423.200

Explicación paso a paso:

para resolver el ejercicio se asumirá que la altura de las columnas tienen una altura de 227 metros.

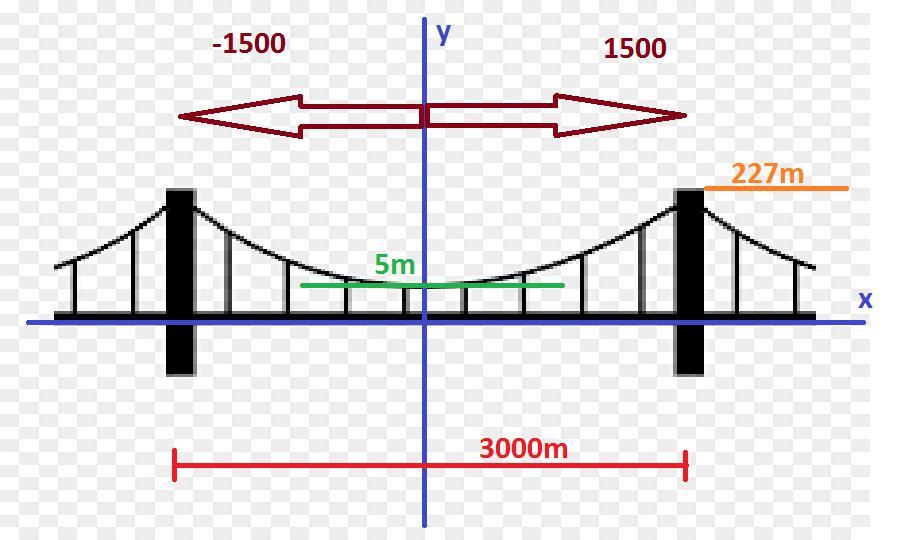
la parábola que forma el puente se ve en la figura adjunta.

al colocar la imagen sobre el plano cartesiano vemos que la parábola esta definida entre -1500 y 1500, por lo que la integral quedara:

\int\limits^{1500}_{-1500} {f(x)} \, dx

ahora definiremos la función f(x):

como es una parábola tendrá la forma

f(x)=ax^2+b

de acuerdo a la figura podemos determinar que f(0)=5, por lo que b=5 asi que f(x) será:

f(x)=ax^2+5

ahora, cuando x=1500, la función tendrá una valor de , esto es:

227=ax^2+5

227=a(1500)^2+5

despejaremos a:

227-5=a(1500)^2

222=a(1500)^2

a=\dfrac{222}{1500^2}

a=9,86.10^{-5}

reemplazando tenemos que nuestra función es:

f(x)=9,86.10^{-5}x^2+5

reemplazando en la integral nos da:

\int\limits^{1500}_{-1500} {(9,86.10^{-5}x^2+5)} \, dx

ahora si podemos realizar la integral quedando:

\dfrac{9,86.10^{-5}x^3}{3} +5x \ \ |\limits^{+1500}_{-1500}

ahora evaluaremos la función obtenida en los limites quedando:

\dfrac{9,86.10^{-5}.(1500)^3}{3} +5(1500) -(\dfrac{9,86.10^{-5.}(-1500)x^3}{3} +5(-1500))

118.425-(-118.425)

236.850

como la integral es el área bajo la curva, y los términos usados están en metros, entonces podemos decir que se requiere un total de 236.855 metros cuadrados de malla para cubrir uno de los lados del puente.

para cubrir el otro lado, se necesitara una cantidad igual a la calculada, es decir 236.850 metros cuadrados de malla.

la malla total será

236.850m^2+236.850m^2=473.700m^2

por lo tanto, se requieren 473.700 metros cuadrados de malla

finalmente vamos a calcular el costo total de la malla requerida para hacer el cerramiento:

vamos a multiplicar el costo del metro cuadrado de malla por el total de metros cuadrados, esto es:

Valor \ total=\$ 136/m^2 \times 473.700m^2

Valor \ total = \$ 64'423.200

por lo tanto, el costo total de la malla requerida es $64'423.200