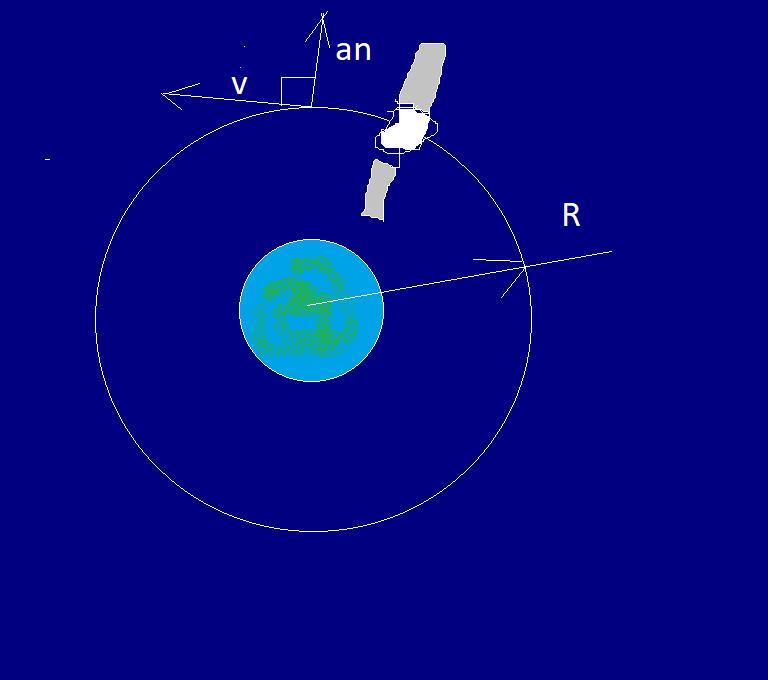
Un satélite gira en una orbita circular alrededor de la tierra y lleva una rapidez circunferencial de 6200 m/seg. Calcular a) A que altura sobre la superficie de la tierra gira b) ¿cual es la longitud de la orbita c) ¿cual es la rapidez angular d) ¿cual es la aceleración centrípeta

Respuestas 1

Sobre este movimiento circular uniforme tenemos:

a) La altura del satélite sobre la superficie terrestre es de 3998 km;

b) La longitud de la órbita es de 6,52\times 10^7m;

c) La rapidez angular es de 5,98\times 10^{-4}s^{-1};

d) La aceleración centrípeta del satélite es de 3,7 metros por segundo cuadrado.

¿Cómo hallar la altitud del satélite teniendo la velocidad?

El satélite se mantiene en órbita donde la fuerza centrípeta se iguala con la fuerza gravitatoria sobre el satélite:

\frac{mv^2}{R}=G\frac{M\cdot m}{R^2}\\\\v^2=G\frac{ m}{R}

De esta expresión podemos despejar el radio de la órbita:

R=G\frac{M}{v^2}=6,67\times 10^{-11}\frac{Nm^2}{kg^2}\frac{5,98\times 10^{24}kg}{(6200\frac{m}{s})^2}\\R=10376327m=10376,327km

Como este radio está considerado desde el centro de la Tierra, para hallar la altitud tenemos que restarle el radio de la Tierra:

h=10376,327km-6378km=3998,327km

¿Cómo hallar la longitud de la órbita del satélite?

Teniendo el radio de la órbita del satélite, podemos hallar la longitud de la órbita suponiéndola circular:

L=2\pi R=2\pi\cdot 10376,327km=6,52\times 10^{7}m

¿Cómo hallar la rapidez angular y la aceleración centrípeta?

Teniendo la velocidad tangencial, podemos hallar la velocidad angular del satélite:

w=\frac{v}{R}=\frac{6200\frac{m}{s}}{10376327m}=5,98\times 10^{-4}s^{-1}

La aceleración centrípeta es:

a_n=w^2R=(5,98\times 10^{-4}s^{-1})^2\cdot 10376327m=3,7\frac{m}{s^2}

Aprende más sobre el movimiento circular uniforme en https://brainly.lat/tarea/11823442

#SPJ1