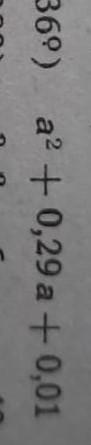Definicion caja de mecanismos ‼️‼️ Responder ya

Respuesta:

Supongo que quisiste poner

1). x^1 - 2x^2 + 3x = 10

2). 4x^1 - x^2 + x^3 = 4

3). 2x^1 - x^2 + 3x^3 = 10

Respuesta:

\Large{\boxed{a^2+0.29a+0.01=(a+\frac{1}{4} )(a+\frac{1}{25} )}}

Explicación paso a paso:

a^2+0,29a+0,01

primero vamos eliminar los decimales de los términos 2 y 3

para ello multiplicaremos toda la expresión por 100 obteniendo:

100(a^2+0,29a+0,01)

resolvemos:

100a^2+29a+1

ahora tenemos un polinomio de la forma ax^2+bx+c.

donde

a=100

b=29

c=1

Para resolverlo, multiplicaremos y dividiremos todos los términos por 100:

\dfrac{100(100a^2+29a+1)}{100}

resolvemos el numerador así:

\dfrac{100^2a^2+29(100)a+100)}{100}

\dfrac{(100a)^2+29(100a)+100}{100}

ahora el numerador es de la forma x^2+bx+c y lo podemos escribir así:

\dfrac{(100a+e)(100a+f)}{100}

vamos a buscar dos números e y f que sumados den 29 y multiplicados den 100.

los números son:

e = 25

f = 4

reemplazamos quedando:

\dfrac{(100a+25)(100a+4)}{100}

sacamos factor común en los términos del numerador:

\dfrac{25(4a+1) \times 4(25a+1)}{100}

lo que es igual a:

\dfrac{100(4a+1)(25a+1)}{100}

eliminamos el 100 del numerador y denominador quedando:

(4a+1)(25a+1)

como inicialmente habíamos multiplicado por 100 para eliminar los decimales, ahora debemos volver a dividir entre 100 para que no se altere la expresión :

\dfrac{(4a+1)(25a+1)}{100}

como 100 = 25 x 4 reemplazamos:

\dfrac{(4a+1)(25a+1)}{4 \times 25}

dividimos el primer termino entre 4 y el segundo entre 25 quedando:

\dfrac{(4a+1)}{4}.\dfrac{(25a+1)}{25}

lo que es igual a:

(a+\frac{1}{4} )(a+\frac{1}{25} )

por lo tanto:

\Large{\boxed{a^2+0.29a+0.01=(a+\frac{1}{4} )(a+\frac{1}{25} )}}

Respuesta:

primer cociente: 17,155

resto: 3

dividendo: 46,184

segundo cociente: 548

Respuesta:

Explicación paso a paso:

En la imagen adjunta se encuentra el cuadro con los datos requeridos.