me ayudan con esto me dan los resultados es que no le entiendo por favor QUIERO EL RESULTADO SI NO SE LA SABEN FAVOR DE NO COMENTAR AYUDAA​

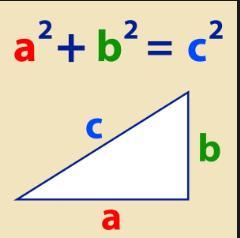
Para desarrollar problemas básicos de triangulo rectángulos, se utiliza un teorema conocido como "el teorema de Pitágoras" , el cual se utiliza cuando conoces la medidas de 2 lados de un triángulo y cuando el tríangulo es siempre un "tríangulo rectangulo".

Teorema de Pitágoras.

a^{2} +b^{2} =c^{2}

Donde :

a= es uno de los lados (no puede ser la hipotenusa).

b= es otro de los lados (No puede ser la hipotenusa,pero tampoco debe ser el mismo lado que "a",pero puede medir igual que "a")

c= Es la hipotenusa (El lado más largo del triángulo)

Resolviendo tu problema por medio de este teorema básico.

1.-

a^{2} +b^{2} =c^{2}

reemplazando los valores :

a^{2} +6^{2} =10^{2}

a^{2} +36 =100

Ahora, sumamos "-36" a ambos lados para quitar el "36" del lado izquierdo y dejar solo a la variable elevada al cuadrado.

a^{2} +36-36 =100-36

a^{2} =64

Ahora procedemos a sacar la raiz cuadrada a ambos lados, pero con la certeza que el valor de "a" es un número positivo, pues no existen "medidas negativas".

a^{2} =64

\sqrt{a^{2}} =\sqrt{64}

a =8

Con esto ya tenemos el valor de "a" el cual es 8.

para comprobar solo basta con reemplazar el valor de "a" en el teorema de pitagoras para verificar si la ecuación es verdad.

Problema 2:

Aplicamos el mismo teorema, pero esta vez es otor lado es que nos piden, asi que poner atención en ese detalle.

Reemplazando los valores en la formula del teorema:

a^{2} +b^{2} =c^{2}

4^{2} +3^{2} =c^{2}

Efectuando la operacióm:

16 +9 =c^{2}

25 =c^{2}

Ahora sacamos la raíz cuadrada a ambos lados, con la certeza que "c" es un numero positivo.

25 =c^{2}

\sqrt{25}= \sqrt{c^{2}}

5 = c

Ya obtuvimos el valor de "c" el cual es 5.

Problema 3:

Aplicamos el mismo teorema .

a^{2} +b^{2} =c^{2}

a^{2}+3^{2} =5^{2}

a^{2} +9 =25

Ahora sumamos "-9" a ambos lados para quitar el "9" del lado izquierdo y para dejar solito a la variable "a^{2}".

a^{2} +9 =25

a^{2} +9-9 =25-9

a^{2} =16

Sacamos la raiz cuadrado de ambos lados, con al certeza que el valor de "a" es positivo, pues no existe medidas negativas en geometría.

\sqrt{ a^{2}}= \sqrt{16}

a = 4

espero haberte ayudado, si hay algún error de antemano pido disculpas.