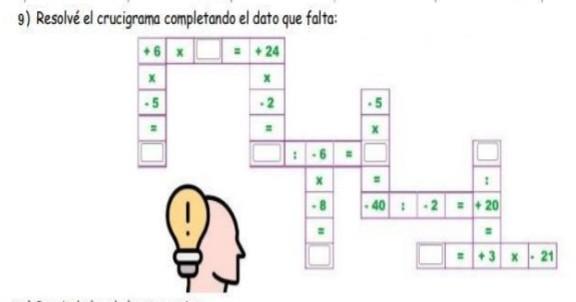
9) Resolvé el gráfico completando el dato que falta:POR FAVORRR, NECESITO APROBAR. DOY CORONADO
-
Materia:
Matemáticas -
Autor/a:
ladybug24 -
Creada:
hace 1 año
Respuestas 2
Respuesta:
5x8= 40
6x5=30
6x4=24+24=48
24x2=48
solo eso me se bro, esque no puedo ver bien la imagen,
-
Autor/a:
braylonqy5f
-
Califica una respuesta:
2
Respuesta:
-30,+4,-48,+8,+60,-63
Explicación paso a paso:
se trata de ley de signos
+×+=+
+×-=-
-×-=+
-×+=-
-
Autor/a:
cheyennei7kw
-
Califica una respuesta:
19
¿Conoces la respuesta? Añádela aquí
Escoger idioma y región
How much to ban the user?
1 hour
1 day
100 years

