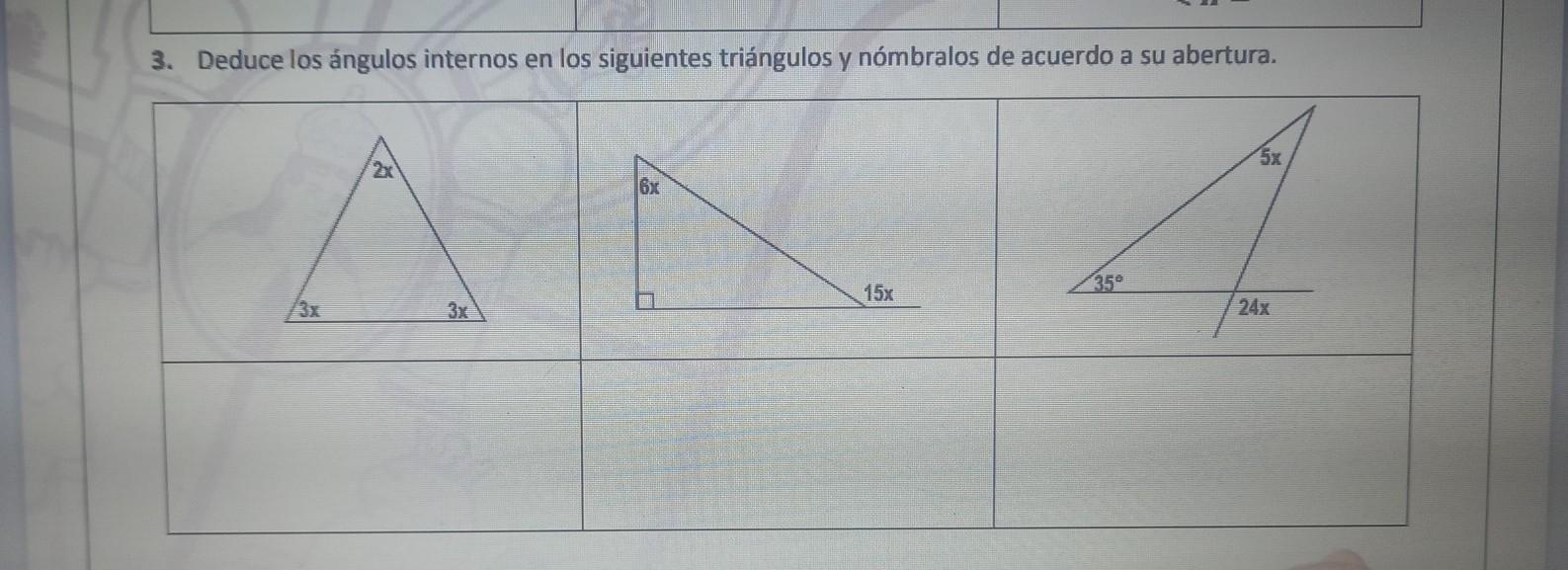
3. Deduce los ángulos internos en los siguientes triángulos y nómbralos de acuerdo a su abertura. AYUDAAAA
-
Materia:
Matemáticas -
Autor/a:
caylen -
Creada:
hace 1 año
Respuestas 1
Respuesta:1.23 2.32.3e6
Explicación paso a paso:
-
Autor/a:
flashbeps
-
Califica una respuesta:
0
¿Conoces la respuesta? Añádela aquí
Escoger idioma y región
How much to ban the user?
1 hour
1 day
100 years

