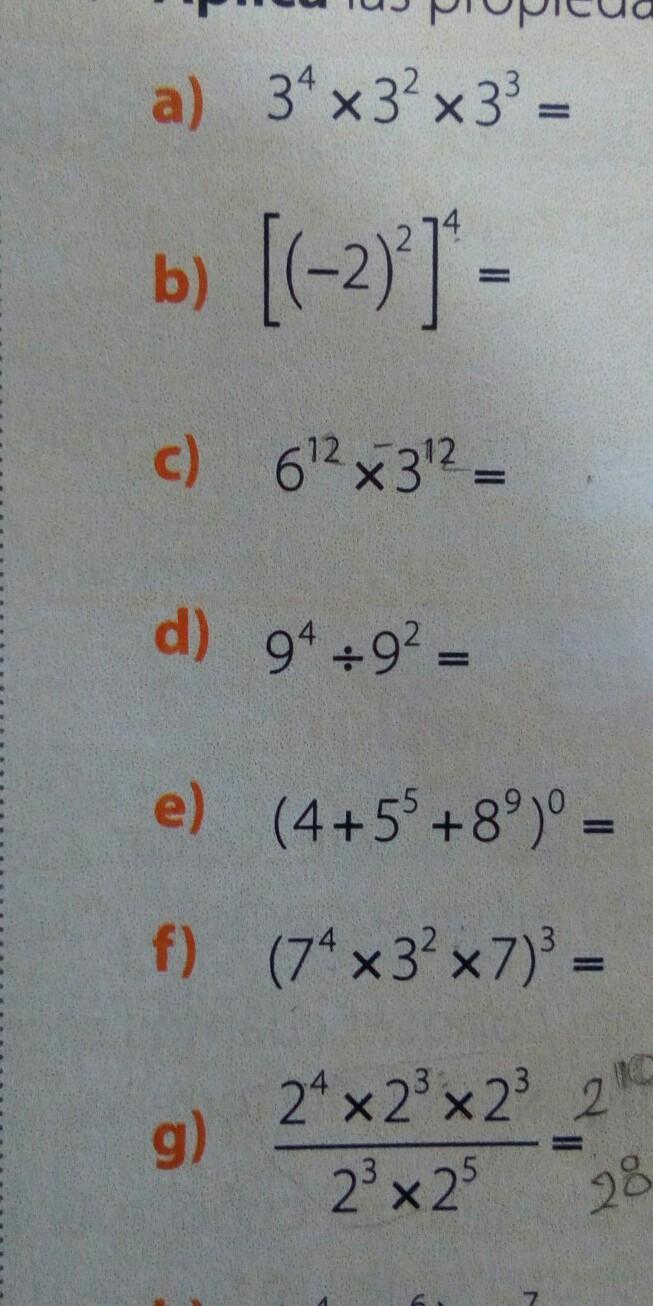ES URGENTE PORFAVOR, ALGUIEN BUENO AYUDEME PLIS.
-
Materia:
Matemáticas -
Autor/a:
aureliano -
Creada:
hace 1 año
Respuestas 2
Respuesta:
Explicación paso a paso:
Hallamos el área para (1;1)
A=2x²+5xy+3y²
A=2(1²)+5(1).(1)+3(1²)
A=2+5+3
A=10u²
Pero como piden hallar P dividimos el área total por el lado (x+y) en u
luego
P=10u²/(1+1)u
P=10u²/2u
P=5u
Respuesta
5u
-
Autor/a:
zackery2pbz
-
Califica una respuesta:
16
Respuesta:
5u
Explicación paso a paso:
Debes recordar la forma básica del área de un rectangulo, siendo base por altura, con términos generales te queda que es P(x;y) por (x+y). Igualas eso a la área, y despejas P(x;y). Pues quieres saber cuánto es P(1;1):
A=B*h\\2x^2+5xy+3y^2=P_{(x;y)}*(x+y)\\\\P_{(x;y)}=\frac{2x^2+5xy+3y^2}{x+y} \\
Puedes hacer esa expresión más chica, pero por motivos de tiempo y en base a lo que te pide, realmente no se ocupa reducirlo. Para saber cuánto es P(1;1), solo remplazas la letra "x" y la "y" por el número 1:
P_{(x;y)}=\frac{2x^2+5xy+3y^2}{x+y} \\\\\\P(1;1)=\frac{2(1)^2+5(1)(1)+3(1)^2}{1+1} =\frac{10}{2}=5u
-
Autor/a:
estermoreno
-
Califica una respuesta:
8
¿Conoces la respuesta? Añádela aquí
Other related questions that may help you
-
Autor/a:
allisson
-
Autor/a:
tiarapollard
-
Califica una respuesta:
5
-
Autor/a:
addie
-
Autor/a:
cassiemduz
-
Califica una respuesta:
9
-
Autor/a:
rolandojcuz
-
Califica una respuesta:
17
-
Autor/a:
romeobowers
Respuesta:
el radio es un medio de comunicación que se basa en el envío de señales de audio a través de ondas de radio, si bien el término se usa también para otras formas de envío de audio a distancia como la radio por Internet.
-
Autor/a:
tomc5cr
-
Califica una respuesta:
5